Projection Parameters
Every projection has at least one parameter that controls how it transforms geographic coordinates into planar coordinates. Some projections are rather fixed, and aside from the orientation vector and nominal scale factor, have no parameters that the user should vary, as to do so would violate the definition of the projection. For example, the Robinson projection has one standard parallel that is fixed by definition at 38° North and South; the Cassini and Wetch projections cannot be constructed in other than Normal aspect. In general, however, projections have several variable parameters. The following section discusses map projection parameters and provides guidance for setting them.
Projection Characteristics Maps Can Have
In addition to the name of the projection itself, the parameters that a map projection can have are
Aspect — Orientation of the projection on the display surface
Center or Origin — Latitude and longitude of the midpoint of the display
Scale Factor — Ratio of distance on the map to distance on the ground
Standard Parallel(s) — Chosen latitude(s) where scale distortion is zero
False Northing — Planar offset for coordinates on the vertical map axis
False Easting — Planar offset for coordinates on the horizontal map axis
Zone — Designated latitude-longitude quadrangle used to systematically partition the planet for certain classes of projections
While not all projections require all these parameters, there will always be a projection aspect, origin, and scale.
Other parameters are associated with the graphic expression of a projection, but do not define its mathematical outcome. These include
Map latitude and longitude limits
Frame latitude and longitude limits
However, as certain projections are unable to map an entire planet, or become very distorted over large regions, these limits are sometimes a necessary part of setting up a projection.
Determining Projection Parameters
In the following exercise, you define an axesm-based map and
examine default parameters for a cylindrical, a conic, and an azimuthal projection.
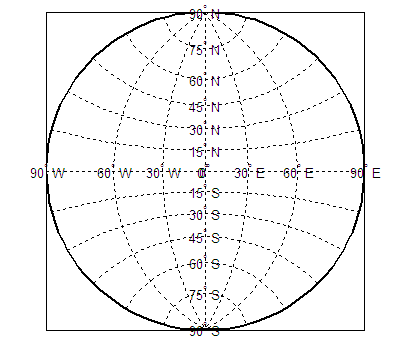
Set up a default Mercator projection (which is cylindrical) and pass its handle to the
getmfunction to query projection parameters:figure; h=axesm('Mapprojection','mercator','Grid','on','Frame','on',... 'MlabelParallel',0,'PlabelMeridian',0,'mlabellocation',60,... 'meridianlabel','on','parallellabel','on')The graticule and frame for the default map projection are shown below.
Query the handle of the
axesm-based map usinggetmto inspect the properties that pertain to map projection parameters. The principal ones areaspect,origin,scalefactor,nparallels,mapparallels,falsenorthing,falseeasting,zone,maplatlimit,maplonlimit,rlatlimit, andflonlimit:getm(h,'aspect') ans = normal getm(h,'origin') ans = 0 0 0 getm(h,'scalefactor') ans = 1 getm(h,'nparallels') ans = 1 getm(h,'mapparallels') ans = 0 getm(h,'falsenorthing') ans = 0 getm(h,'falseeasting') ans = 0 getm(h,'zone') ans = [] getm(h,'maplatlimit') ans = -86 86 getm(h,'maplonlimit') ans = -180 180 getm(h,'Flatlimit') ans = -86 86 getm(h,'Flonlimit') ans = -180 180For more information on these and other properties of
axesm-based maps, see axesm-Based Map Properties.Reset the projection type to equal-area conic (
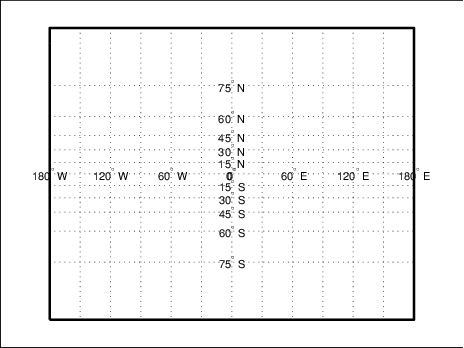
'eqaconic'). The figure is redrawn to reflect the change. Determine the parameters that the toolbox changes in response:setm(h,'Mapprojection', 'eqaconic') getm(h,'aspect') ans = normal getm(h,'origin') ans = 0 0 0 getm(h,'scalefactor') ans = 1 getm(h,'nparallels') ans = 2 getm(h,'mapparallels') ans = 15 75 getm(h,'falsenorthing') ans = 0 getm(h,'falseeasting') ans = 0 getm(h,'zone') ans = [] getm(h,'maplatlimit') ans = -86 86 getm(h,'maplonlimit') ans = -135 135 getm(h,'Flatlimit') ans = -86 86 getm(h,'Flonlimit') ans = -135 135The
eqaconicprojection has two standard parallels, at 15° and 75°. It also has reduced longitude limits (covering 270° rather than 360°). The resultingeqaconicgraticule is shown below.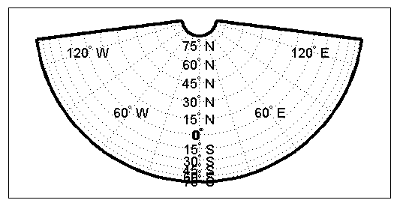
Now set the projection type to Stereographic (
'stereo') and examine the same properties as you did for the previous projections:setm(h,'Mapprojection','stereo') setm(gca,'MLabelParallel',0,'PLabelMeridian',0) getm(h,'aspect') ans = normal getm(h,'origin') ans = 0 0 0 getm(h,'scalefactor') ans = 1 getm(h,'nparallels') ans = 0 getm(h,'mapparallels') ans = [] getm(h,'falsenorthing') ans = 0 getm(h,'falseeasting') ans = 0 getm(h,'zone') ans = [] getm(h,'maplatlimit') ans = -90 90 getm(h,'maplonlimit') ans = -180 180 getm(h,'Flatlimit') ans = -Inf 90 getm(h,'Flonlimit') ans = -180 180The stereographic projection, being azimuthal, does not have standard parallels, so none are indicated. The map limits do not change from the previous projection. The map figure is shown below.