areaquad
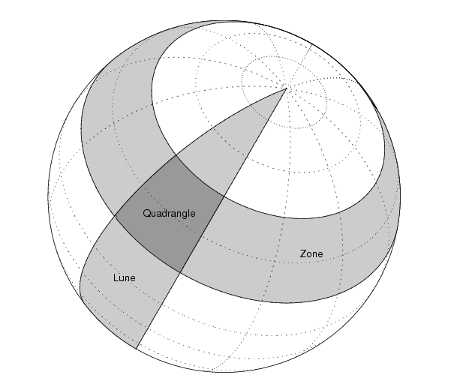
Surface area of latitude-longitude quadrangle
Syntax
Description
Examples
Input Arguments
Output Arguments
More About
Algorithms
The
areaquadfunction uses spherical geometry and returns exact calculations.When you specify
ellipsoidas a nonspherical ellipsoid, the function converts the latitude data to the auxiliary authalic sphere.
Version History
Introduced before R2006a