scircle2
Small circle from center and point on perimeter
Syntax
Description
[
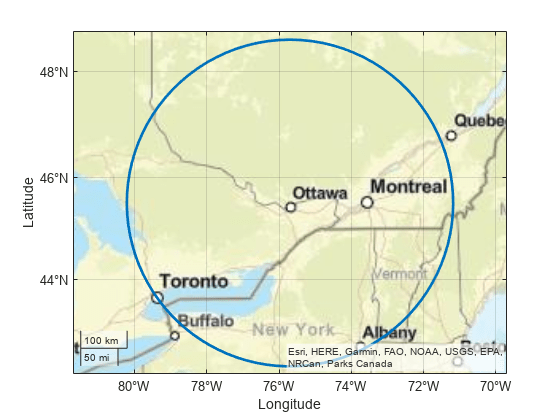
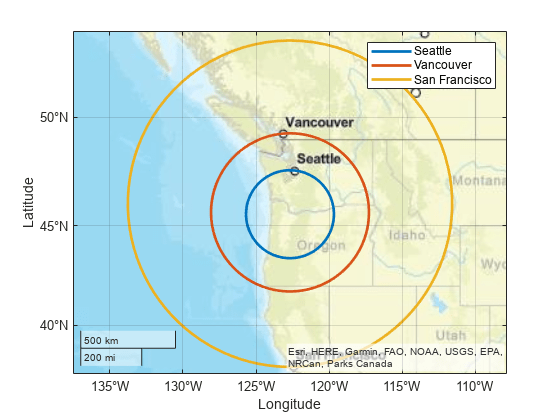
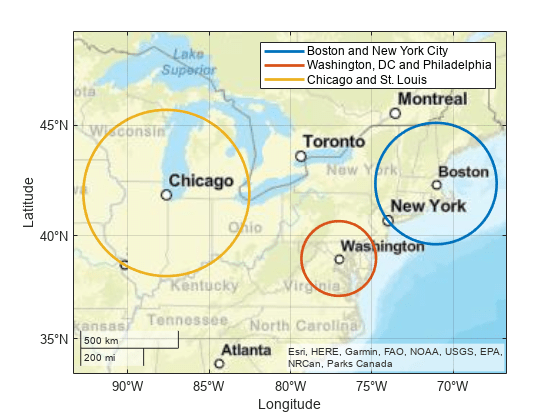
finds the latitude and longitude coordinates of a small circle. Specify the geographic
coordinates of the center of the small circle using lat,lon] = scircle2(lat0,lon0,latP,lonP)lat0 and
lon0. Specify a point on the perimeter of the small circle using
latP and lonP. This syntax assumes that the
coordinates are referenced to a sphere.
[,
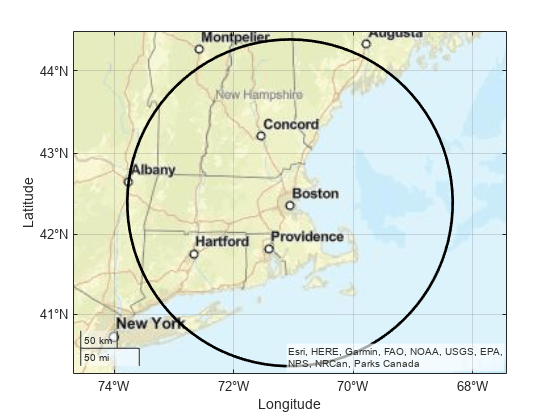
where lat,lon] = scircle2(method,___)method is "rh", specifies that distances from
the center of the small circle are rhumb line distances. The default for
method is "gc", which specifies that distances
from the center of the small circle are great circle distances (for a sphere) or geodesic
distances (for an ellipsoid).
mat = scircle2(___)mat.
Examples
Input Arguments
Output Arguments
More About
Version History
Introduced before R2006a