Anonymous Functions
What Are Anonymous Functions?
An anonymous function is a function that is not stored in a
program file, but is associated with a variable whose data type is
function_handle
Note
You can create an anonymous function that returns multiple outputs using the
deal function. See Return Multiple Outputs from Anonymous Function for an
example.
For example, create a handle to an anonymous function that finds the square of a number:
sqr = @(x) x.^2;
Variable sqr is a function handle. The @
operator creates the handle, and the parentheses () immediately
after the @ operator include the function input arguments. This
anonymous function accepts a single input x, and implicitly
returns a single output, an array the same size as x that
contains the squared values.
Find the square of a particular value (5) by passing the value
to the function handle, just as you would pass an input argument to a standard
function.
a = sqr(5)
a = 25
Many MATLAB® functions accept function handles as inputs so that you can evaluate functions over a range of values. You can create handles either for anonymous functions or for functions in program files. The benefit of using anonymous functions is that you do not have to edit and maintain a file for a function that requires only a brief definition.
For example, find the integral of the sqr function from
0 to 1 by passing the function handle to
the integral function:
q = integral(sqr,0,1);
You do not need to create a variable in the workspace to store an anonymous
function. Instead, you can create a temporary function handle within an expression,
such as this call to the integral function:
q = integral(@(x) x.^2,0,1);
Variables in the Expression
Function handles can store not only an expression, but also variables that the expression requires for evaluation.
For example, create a handle to an anonymous function that requires coefficients
a, b, and c.
a = 1.3; b = .2; c = 30; parabola = @(x) a*x.^2 + b*x + c;
Because a, b, and c are
available at the time you create parabola, the function handle
includes those values. The values persist within the function handle even if you
clear the variables:
clear a b c x = 1; y = parabola(x)
y = 31.5000
To supply different values for the coefficients, you must create a new function handle:
a = -3.9; b = 52; c = 0; parabola = @(x) a*x.^2 + b*x + c; x = 1; y = parabola(x)
y = 48.1000
You can save function handles and their associated values in a MAT-file and load
them in a subsequent MATLAB session using the save and load
functions, such as
save myfile.mat parabola
Use only explicit variables when constructing anonymous functions. If an anonymous
function accesses any variable or nested function that is not explicitly referenced
in the argument list or body, MATLAB throws an error when you invoke the function. Implicit variables and
function calls are often encountered in the functions such
as eval, evalin,
assignin, and load. Avoid
using these functions in the body of anonymous functions.
Multiple Anonymous Functions
The expression in an anonymous function can include another anonymous function. This is useful for passing different parameters to a function that you are evaluating over a range of values. For example, you can solve the equation
![]()
for varying values of c by combining two anonymous
functions:
g = @(c) (integral(@(x) (x.^2 + c*x + 1),0,1));
Here is how to derive this statement:
Write the integrand as an anonymous function,
@(x) (x.^2 + c*x + 1)
Evaluate the function from zero to one by passing the function handle to
integral,integral(@(x) (x.^2 + c*x + 1),0,1)
Supply the value for
cby constructing an anonymous function for the entire equation,g = @(c) (integral(@(x) (x.^2 + c*x + 1),0,1));
The final function allows you to solve the equation for any value of
c. For example:
g(2)
ans = 2.3333
Functions with No Inputs
If your function does not require any inputs, use empty parentheses when you define and call the anonymous function. For example:
t = @() datestr(now); d = t()
d = 26-Jan-2012 15:11:47
Omitting the parentheses in the assignment statement creates another function handle, and does not execute the function:
d = t
d =
@() datestr(now)Functions with Multiple Inputs or Outputs
Anonymous functions require that you explicitly specify the input arguments as you would for a standard function, separating multiple inputs with commas. For example, this function accepts two inputs, x and y:
myfunction = @(x,y) (x^2 + y^2 + x*y); x = 1; y = 10; z = myfunction(x,y)
z = 111
However, an anonymous function returns only one output. If the expression in the function returns multiple outputs, then you can request them when you invoke the function handle.
For example, the ndgrid function can return as many outputs as the number of input vectors. This anonymous function that calls ndgrid returns only one output (mygrid). Invoke mygrid to access the outputs returned by the ndgrid function.
c = 10; mygrid = @(x,y) ndgrid((-x:x/c:x),(-y:y/c:y)); [x,y] = mygrid(pi,2*pi);
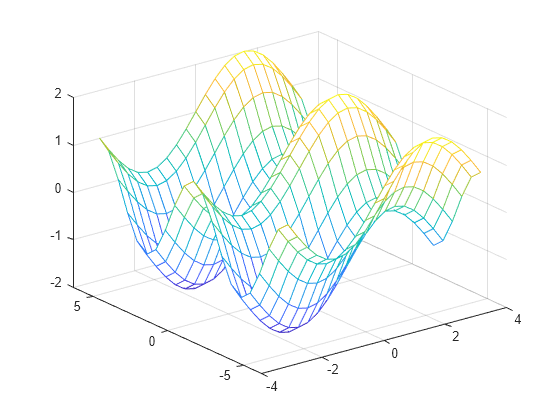
You can use the output from mygrid to create a mesh or surface plot:
z = sin(x) + cos(y); mesh(x,y,z)
Arrays of Anonymous Functions
Although most MATLAB fundamental data types support multidimensional arrays, function handles must be scalars (single elements). However, you can store multiple function handles using a cell array or structure array. The most common approach is to use a cell array, such as
f = {@(x)x.^2;
@(y)y+10;
@(x,y)x.^2+y+10};When you create the cell array, keep in mind that MATLAB interprets spaces as column separators. Either omit spaces from expressions, as shown in the previous code, or enclose expressions in parentheses, such as
f = {@(x) (x.^2);
@(y) (y + 10);
@(x,y) (x.^2 + y + 10)};Access the contents of a cell using curly braces. For example,
f{1} returns the first function handle. To execute the
function, pass input values in parentheses after the curly braces:
x = 1;
y = 10;
f{1}(x)
f{2}(y)
f{3}(x,y)ans =
1
ans =
20
ans =
21