Graphs and Matrices
This example shows an application of sparse matrices and explains the relationship between graphs and matrices.
A graph is a set of nodes with specified connections, or edges, between them. Graphs come in many shapes and sizes. One example is the connectivity graph of the Buckminster Fuller geodesic dome, which is also in the shape of a soccer ball or a carbon-60 molecule.
In MATLAB®, you can use the bucky function to generate the graph of the geodesic dome.
[B,V] = bucky;
G = graph(B);
p = plot(G);
axis equal
You also can specify coordinates for the nodes to change the display of the graph.
p.XData = V(:,1); p.YData = V(:,2);

The bucky function can be used to create the graph because it returns an adjacency matrix. An adjacency matrix is one way to represent the nodes and edges in a graph.
To construct the adjacency matrix of a graph, the nodes are numbered 1 to N. Then each element (i,j) of the N-by-N matrix is set to 1 if node i is connected to node j, and 0 otherwise. Thus, for undirected graphs the adjacency matrix is symmetric, but this need not be the case for directed graphs.
For example, here is a simple graph and its associated adjacency matrix.
% Define a matrix A. A = [0 1 1 0 ; 1 0 0 1 ; 1 0 0 1 ; 0 1 1 0]; % Draw a picture showing the connected nodes. cla subplot(1,2,1); gplot(A,[0 1;1 1;0 0;1 0],'.-'); text([-0.2, 1.2 -0.2, 1.2],[1.2, 1.2, -.2, -.2],('1234')', ... 'HorizontalAlignment','center') axis([-1 2 -1 2],'off') % Draw a picture showing the adjacency matrix. subplot(1,2,2); xtemp = repmat(1:4,1,4); ytemp = reshape(repmat(1:4,4,1),16,1)'; text(xtemp-.5,ytemp-.5,char('0'+A(:)),'HorizontalAlignment','center'); line([.25 0 0 .25 NaN 3.75 4 4 3.75],[0 0 4 4 NaN 0 0 4 4]) axis off tight

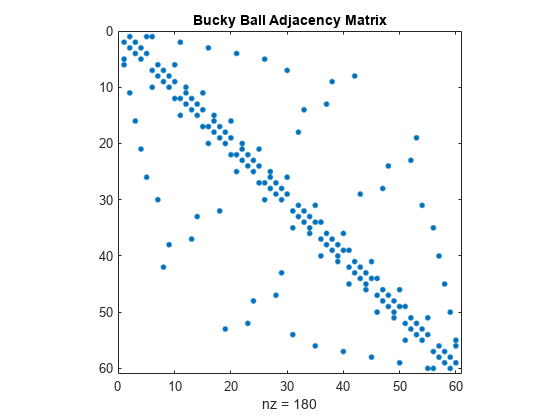
Sparse matrices are particularly helpful for representing very large graphs. This is because each node is usually connected to only a few other nodes. As a result, the density of nonzero entries in the adjacency matrix is often relatively small for large graphs. The bucky ball adjacency matrix is a good example, since it is a 60-by-60 symmetric sparse matrix with only 180 nonzero elements. The density of this matrix is just 5%.
Since the adjacency matrix defines the graph, you can plot a portion of the bucky ball by using a subset of the entries in the adjacency matrix.
Use the adjacency function to create a new adjacency matrix for the graph. Display the nodes in one hemisphere of the bucky ball by indexing into the adjacency matrix to create a new, smaller graph.
figure A = adjacency(G); H = graph(A(1:30,1:30)); h = plot(H);

To visualize the adjacency matrix of this hemisphere, use the spy function to plot the silhouette of the nonzero elements in the adjacency matrix.
Note that the matrix is symmetric, since if node i is connected to node j, then node j is connected to node i.
spy(A(1:30,1:30))
title('Top Left Corner of Bucky Ball Adjacency Matrix')
Finally, here is a spy plot of the entire bucky ball adjacency matrix.
spy(A)
title('Bucky Ball Adjacency Matrix')