Introduction to the Live Editor
This example is an introduction to the Live Editor. In the Live Editor, you can create live scripts that show output together with the code that produced it. Add formatted text, equations, images, and hyperlinks to enhance your narrative, and share the live script with others as an interactive document.
Create a live script in the Live Editor. To create a live script, on the Home tab, click New Live Script.
Add the Census Data
Divide your live script into sections. Sections can contain text, code, and output. MATLAB® code appears with a gray background and output appears with a white background. To create a new section, go to the Live Editor tab and click the Section Break button.
Add the US Census data for 1900 to 2000.
years = (1900:10:2000); % Time interval pop = [75.995 91.972 105.711 123.203 131.669 ... % Population Data 150.697 179.323 213.212 228.505 250.633 265.422]
pop = 1×11
75.9950 91.9720 105.7110 123.2030 131.6690 150.6970 179.3230 213.2120 228.5050 250.6330 265.4220
Visualize the Population Change over Time
Sections can be run independently. To run the code in a section, go to the Live Editor tab and click the Run Section button. You can also click the blue bar that appears when you move the mouse to the left of the section. When you run a section, output and figures appear together with the code that produced them.
Plot the population data against the year.
plot(years,pop,'bo'); % Plot the population data axis([1900 2020 0 400]); title('Population of the U.S. 1900-2000'); ylabel('Millions'); xlabel('Year') ylim([50 300])
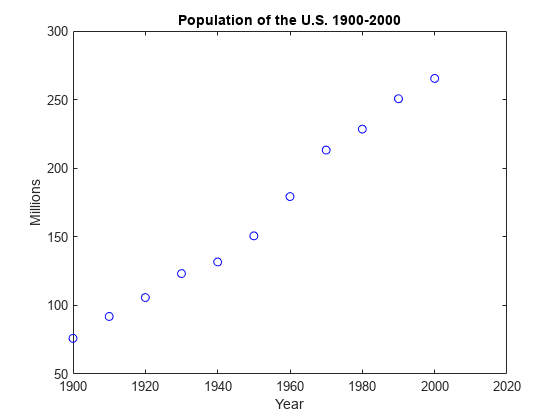
Can we predict the US population in the year 2010?
Fitting the Data
Add supporting information to the text, including equations, images, and hyperlinks.
Let's try fitting the data with polynomials. We'll use the MATLAB polyfit function to get the coefficients.
The fit equations are:
x = (years-1900)/50; coef1 = polyfit(x,pop,1)
coef1 = 1×2
98.9924 66.1296
coef2 = polyfit(x,pop,2)
coef2 = 1×3
15.1014 68.7896 75.1904
coef3 = polyfit(x,pop,3)
coef3 = 1×4
-17.1908 66.6739 29.4569 80.1414
Plotting the Curves
Create sections with any number of text and code lines.
We can plot the linear, quadratic, and cubic curves fitted to the data. We'll use the polyval function to evaluate the fitted polynomials at the points in x.
pred1 = polyval(coef1,x); pred2 = polyval(coef2,x); pred3 = polyval(coef3,x); [pred1; pred2; pred3]
ans = 3×11
66.1296 85.9281 105.7266 125.5250 145.3235 165.1220 184.9205 204.7190 224.5174 244.3159 264.1144
75.1904 89.5524 105.1225 121.9007 139.8870 159.0814 179.4840 201.0946 223.9134 247.9403 273.1753
80.1414 88.5622 101.4918 118.1050 137.5766 159.0814 181.7944 204.8904 227.5441 248.9305 268.2243
Now let's plot the predicted values for each polynomial.
hold on plot(years,pred1) plot(years,pred2) plot(years,pred3) ylim([50 300]) legend({'Data' 'Linear' 'Quadratic' 'Cubic'},'Location', 'NorthWest') hold off
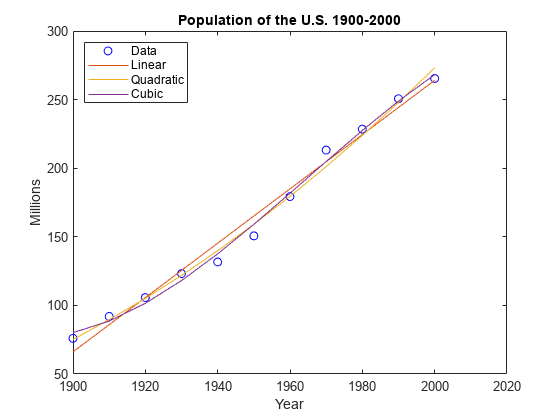
Predicting the Population
You can share your live script with other MATLAB users so that they can reproduce your results. You also can publish your results as PDF, Microsoft® Word, or HTML documents. Add controls to your live scripts to show users how important parameters affect the analysis. To add controls, go to the Live Editor tab, click the Control button, and select from the available options.
We can now calculate the predicted population of a given year using our three equations.
year =  2018;
xyear = (year-1900)/50;
pred1 = polyval(coef1,xyear);
pred2 = polyval(coef2,xyear);
pred3 = polyval(coef3,xyear);
[pred1 pred2 pred3]
2018;
xyear = (year-1900)/50;
pred1 = polyval(coef1,xyear);
pred2 = polyval(coef2,xyear);
pred3 = polyval(coef3,xyear);
[pred1 pred2 pred3]ans = 1×3
299.7517 321.6427 295.0462
For the year 2010 for example, the linear and cubic fits predict similar values of about 284 million people, while the quadratic fit predicts a much higher value of about 300 million people.
