DDE with Constant Delays
This example shows how to use dde23 to solve a system of DDEs (delay differential equations) with constant delays.
The system of equations is
The history function for is constant, .
The time delays in the equations are only present in terms, and the delays themselves are constants, so the equations form a system of constant delay equations.
To solve this system of equations in MATLAB®, you need to code the equations, delays, and history before calling the delay differential equation solver dde23, which is meant for systems with constant delays. You either can include the required functions as local functions at the end of a file (as done here), or save them as separate, named files in a directory on the MATLAB path.
Code Delays
First, create a vector to define the delays in the system of equations. This system has two different delays:
A delay of 1 in the first component .
A delay of 0.2 in the second component .
dde23 accepts a vector argument for the delays, where each element is the constant delay for one component.
lags = [1 0.2];
Code Equation
Now, create a function to code the equations. This function should have the signature dydt = ddefun(t,y,Z), where:
tis time (independent variable).yis the solution (dependent variable).Z(:,j)approximates the delay , where the constant delay is given bylags(j).
These inputs are automatically passed to the function by the solver, but the variable names determine how you code the equations. In this case:
Z(:,1)Z(:,2)
function dydt = ddefun(t,y,Z) ylag1 = Z(:,1); ylag2 = Z(:,2); dydt = [ylag1(1); ylag1(1)+ylag2(2); y(2)]; end
Note: All functions are included as local functions at the end of the example.
Code Solution History
Next, create a function to define the solution history. The solution history is the solution for times .
function s = history(t) s = ones(3,1); end
Solve Equation
Finally, define the interval of integration and solve the DDE using the dde23 solver.
tspan = [0 5]; sol = dde23(@ddefun, lags, @history, tspan);
Plot Solution
The solution structure sol has the fields sol.x and sol.y that contain the internal time steps taken by the solver and corresponding solutions at those times. (If you need the solution at specific points, you can use deval to evaluate the solution at the specific points.)
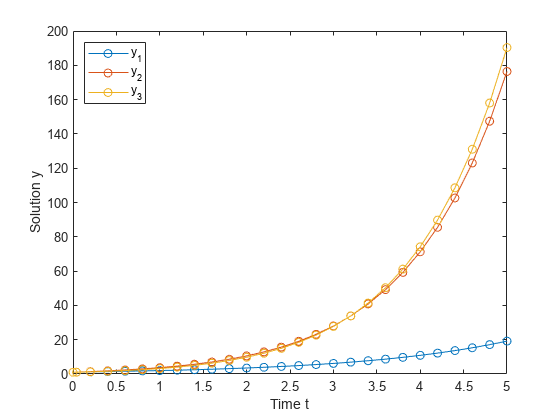
Plot the three solution components against time.
plot(sol.x,sol.y,'-o') xlabel('Time t'); ylabel('Solution y'); legend('y_1','y_2','y_3','Location','NorthWest');
Local Functions
Listed here are the local helper functions that the DDE solver dde23 calls to calculate the solution. Alternatively, you can save these functions as their own files in a directory on the MATLAB path.
function dydt = ddefun(t,y,Z) % equation being solved ylag1 = Z(:,1); ylag2 = Z(:,2); dydt = [ylag1(1); ylag1(1)+ylag2(2); y(2)]; end %------------------------------------------- function s = history(t) % history function for t <= 0 s = ones(3,1); end %-------------------------------------------
See Also
dde23 | ddesd | ddensd | deval
