Fourier Transforms
The Fourier transform is a mathematical formula that transforms a signal sampled in time or space to the same signal sampled in temporal or spatial frequency. In signal processing, the Fourier transform can reveal important characteristics of a signal, namely, its frequency components.
The Fourier transform is defined for a vector with uniformly sampled points by
is one of the complex roots of unity where is the imaginary unit. For and , the indices and range from to .
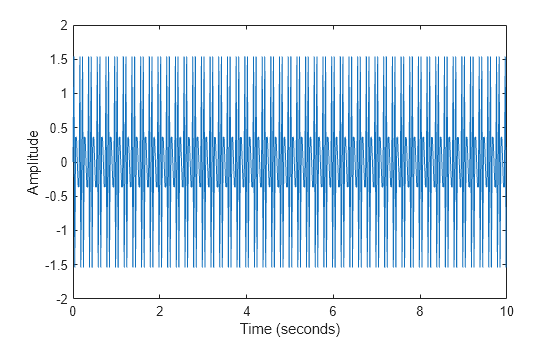
The fft function in MATLAB® uses a fast Fourier transform algorithm to compute the Fourier transform of data. Consider a sinusoidal signal x that is a function of time t with frequency components of 15 Hz and 20 Hz. Use a time vector sampled in increments of 1/50 seconds over a period of 10 seconds.
Ts = 1/50; t = 0:Ts:10-Ts; x = sin(2*pi*15*t) + sin(2*pi*20*t); plot(t,x) xlabel('Time (seconds)') ylabel('Amplitude')
Compute the Fourier transform of the signal, and create the vector f that corresponds to the signal's sampling in frequency space.
y = fft(x); fs = 1/Ts; f = (0:length(y)-1)*fs/length(y);
Plot the magnitude of the transformed signal as a function of frequency.
plot(f,abs(y)) xlabel('Frequency (Hz)') ylabel('Magnitude') title('Magnitude')
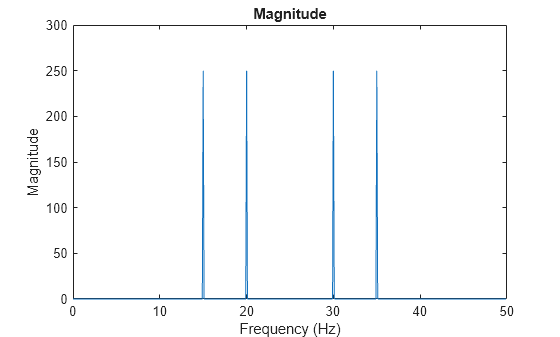
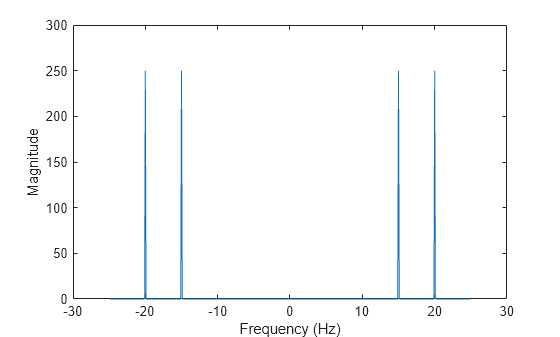
The plot shows four frequency peaks, although the signal is expected to have two frequency peaks at 15 Hz and 20 Hz. Here, the second half of the plot is the mirror reflection of the first half. The discrete Fourier transform of a time-domain signal has a periodic nature, where the first half of its spectrum is in the positive frequencies and the second half is in the negative frequencies. The 30 Hz and 35 Hz frequency components in the plot correspond to the –20 Hz and –15 frequency components. To better visualize this periodicity, you can use the fftshift function, which performs a zero-centered, circular shift on the transform.
n = length(x); fshift = (-n/2:n/2-1)*(fs/n); yshift = fftshift(y); plot(fshift,abs(yshift)) xlabel('Frequency (Hz)') ylabel('Magnitude')
Noisy Signals
In scientific applications, signals are often corrupted with random noise, disguising their frequency components. The Fourier transform can process out random noise and reveal the frequencies. For example, create a new signal, xnoise, by injecting Gaussian noise into the original signal, x.
rng('default')
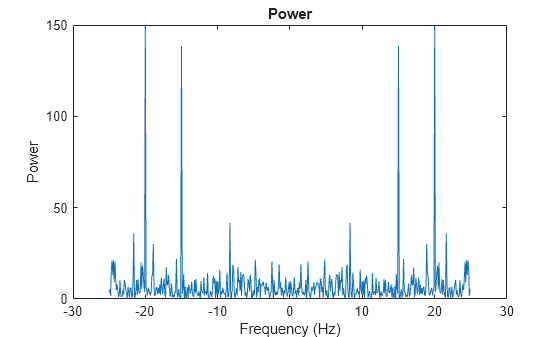
xnoise = x + 2.5*randn(size(t));Signal power as a function of frequency is a common metric used in signal processing. Power is the squared magnitude of a signal's Fourier transform, normalized by the number of frequency samples. Compute and plot the power spectrum of the noisy signal centered at the zero frequency. Despite noise, you can still make out the signal's frequencies due to the spikes in power.
ynoise = fft(xnoise); ynoiseshift = fftshift(ynoise); power = abs(ynoiseshift).^2/n; plot(fshift,power) title('Power') xlabel('Frequency (Hz)') ylabel('Power')
Computational Efficiency
Using the Fourier transform formula directly to compute each of the elements of requires on the order of floating-point operations. The fast Fourier transform algorithm requires only on the order of operations to compute. This computational efficiency is a big advantage when processing data that has millions of data points. Many specialized implementations of the fast Fourier transform algorithm are even more efficient when has small prime factors, such as is a power of 2.
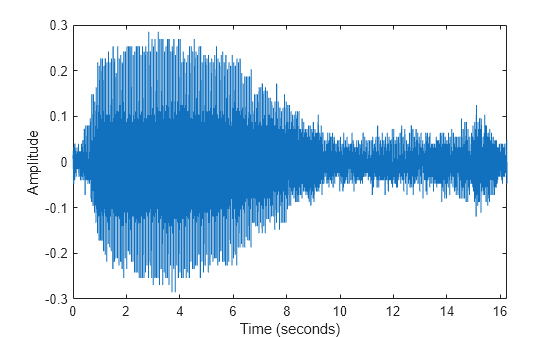
Consider audio data collected from underwater microphones off the coast of California. This data can be found in a library maintained by the Cornell University Bioacoustics Research Program. Load and format a subset of the data in bluewhale.au, which contains a Pacific blue whale vocalization. Because blue whale calls are low-frequency sounds, they are barely audible to humans. The time scale in the data is compressed by a factor of 10 to raise the pitch and make the call more clearly audible. You can use the command sound(x,fs) to listen to the entire audio file.
whaleFile = 'bluewhale.au'; [x,fs] = audioread(whaleFile); whaleMoan = x(2.45e4:3.10e4); t = 10*(0:1/fs:(length(whaleMoan)-1)/fs); plot(t,whaleMoan) xlabel('Time (seconds)') ylabel('Amplitude') xlim([0 t(end)])
Specify a new signal length that is the next power of 2 greater than the original length. Then, use fft to compute the Fourier transform using the new signal length. fft automatically pads the data with zeros to increase the sample size. This padding can make the transform computation significantly faster, particularly for sample sizes with large prime factors.
m = length(whaleMoan); n = pow2(nextpow2(m)); y = fft(whaleMoan,n);
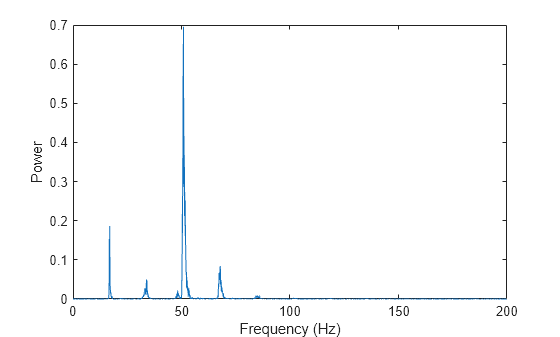
Plot the power spectrum of the signal. The plot indicates that the moan consists of a fundamental frequency around 17 Hz and a sequence of harmonics, where the second harmonic is emphasized.
f = (0:n-1)*(fs/n)/10; % frequency vector power = abs(y).^2/n; % power spectrum plot(f(1:floor(n/2)),power(1:floor(n/2))) xlabel('Frequency (Hz)') ylabel('Power')
Phase of Sinusoids
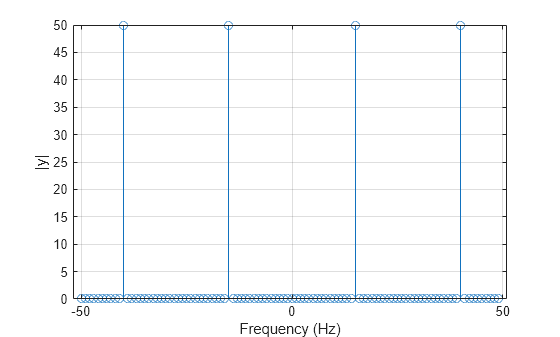
Using the Fourier transform, you can also extract the phase spectrum of the original signal. For example, create a signal that consists of two sinusoids of frequencies 15 Hz and 40 Hz. The first sinusoid is a cosine wave with phase , and the second is a cosine wave with phase . Sample the signal at 100 Hz for 1 second.
fs = 100; t = 0:1/fs:1-1/fs; x = cos(2*pi*15*t - pi/4) - sin(2*pi*40*t);
Compute the Fourier transform of the signal. Plot the magnitude of the transform as a function of frequency.
y = fft(x); z = fftshift(y); ly = length(y); f = (-ly/2:ly/2-1)/ly*fs; stem(f,abs(z)) xlabel("Frequency (Hz)") ylabel("|y|") grid
Compute the phase of the transform, removing small-magnitude transform values. Plot the phase as a function of frequency.
tol = 1e-6; z(abs(z) < tol) = 0; theta = angle(z); stem(f,theta/pi) xlabel("Frequency (Hz)") ylabel("Phase / \pi") grid

See Also
fft | fftshift | nextpow2 | ifft | fft2 | fftn | fftw
