Roots of Polynomials
This example shows several different methods to calculate the roots of a polynomial.
Numeric Roots
The roots function calculates
the roots of a single-variable polynomial represented by a vector
of coefficients.
For example, create a vector to represent the polynomial , then calculate the roots.
p = [1 -1 -6]; r = roots(p)
r =
3
-2By convention, MATLAB® returns the roots in a column vector.
The poly function converts
the roots back to polynomial coefficients. When operating on vectors, poly and roots are
inverse functions, such that poly(roots(p)) returns p (up
to roundoff error, ordering, and scaling).
p2 = poly(r)
p2 =
1 -1 -6When operating on a matrix, the poly function
computes the characteristic polynomial of the matrix. The roots of
the characteristic polynomial are the eigenvalues of the matrix. Therefore, roots(poly(A)) and eig(A) return
the same answer (up to roundoff error, ordering, and scaling).
Roots Using Substitution
You can solve polynomial equations involving trigonometric functions by simplifying the equation using a substitution. The resulting polynomial of one variable no longer contains any trigonometric functions.
For example, find the values of that solve the equation
Use the fact that to express the equation entirely in terms of sine functions:
Use the substitution to express the equation as a simple polynomial equation:
Create a vector to represent the polynomial.
p = [-3 -1 6];
Find the roots of the polynomial.
r = roots(p)
r = 2×1
-1.5907
1.2573
To undo the substitution, use . The asin function calculates the inverse sine.
theta = asin(r)
theta = 2×1 complex
-1.5708 + 1.0395i
1.5708 - 0.7028i
Verify that the elements in theta are the values of that solve the original equation (within round-off error).
f = @(Z) 3*cos(Z).^2 - sin(Z) + 3; f(theta)
ans = 2×1 complex
10-14 ×
-0.0888 + 0.0647i
0.2665 + 0.0399i
Roots in a Specific Interval
Use the fzero function to find the roots of a polynomial in a specific interval. Among other uses, this method is suitable if you plot the polynomial and want to know the value of a particular root.
For example, create a function handle to represent the polynomial .
p = @(x) 3*x.^7 + 4*x.^6 + 2*x.^5 + 4*x.^4 + x.^3 + 5*x.^2;
Plot the function over the interval .
x = -2:0.1:1; plot(x,p(x)) ylim([-100 50]) grid on hold on
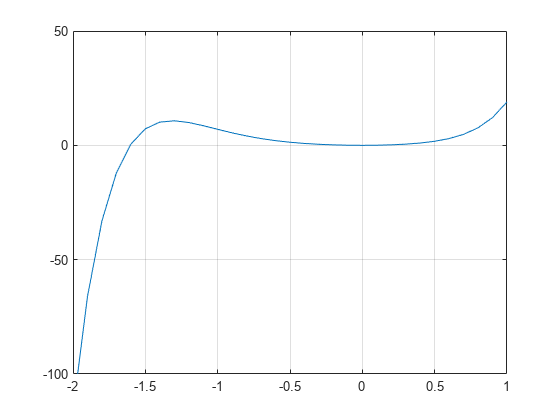
From the plot, the polynomial has a trivial root at 0 and another near -1.5. Use fzero to calculate and plot the root that is near -1.5.
Z = fzero(p, -1.5)
Z = -1.6056
plot(Z,p(Z),'r*')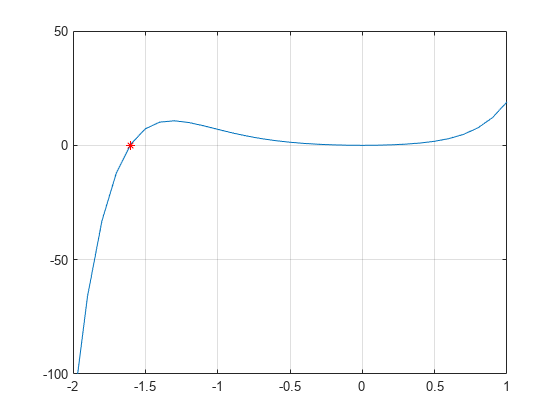
Symbolic Roots
If you have Symbolic Math Toolbox™, then there are additional
options for evaluating polynomials symbolically. One way is to use
the solve (Symbolic Math Toolbox) function.
syms x
s = solve(x^2-x-6)
s = -2 3
Another way is to use the factor (Symbolic Math Toolbox) function
to factor the polynomial terms.
F = factor(x^2-x-6)
F = [ x + 2, x - 3]
See Solve Algebraic Equations (Symbolic Math Toolbox) for more information.
