besselh
Bessel function of third kind (Hankel function)
Description
H = besselh(
computes the Hankel function of the first kind for each element in array nu,Z)Z.
H = besselh(
computes the Hankel function of the first or second kind , where nu,K,Z)K is 1 or
2, for each element of array Z.
Examples
Modulus and Phase of Hankel Function
Generate the contour plots of the modulus and phase of the Hankel function [1].
Create a grid of values for the domain.
[X,Y] = meshgrid(-4:0.002:2,-1.5:0.002:1.5);
Calculate the Hankel function over this domain and generate the modulus contour plot.
H = besselh(0,X+1i*Y);
contour(X,Y,abs(H),0:0.2:3.2)
hold on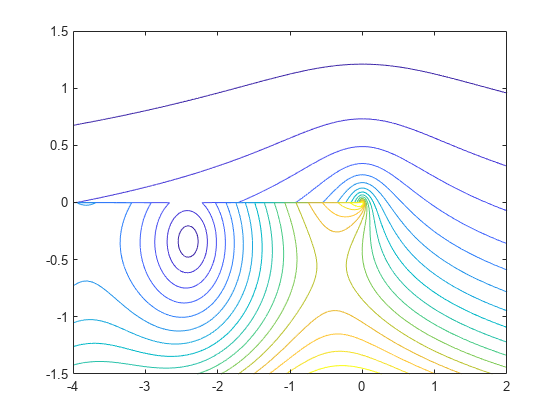
In the same figure, add the contour plot of the phase.
contour(X,Y,rad2deg(angle(H)),-180:10:180)
hold off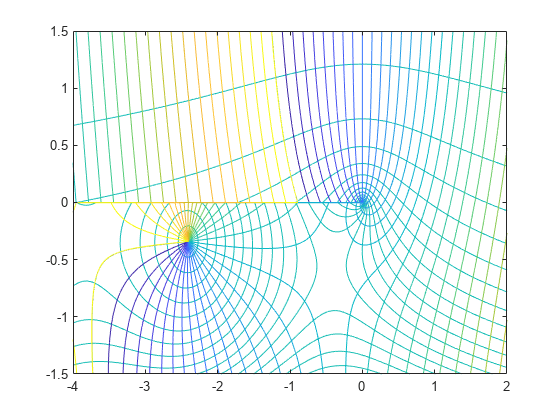
Asymptotic Behavior
Plot the real and imaginary parts of the Hankel function of the second kind and examine their asymptotic behavior.
Calculate the Hankel function of the second kind in the interval .
k = 2; nu = 0; z = linspace(0.1,25,200); H = besselh(nu,k,z);
Plot the real and imaginary parts of the function. In the same figure, plot the linear combination , which reveals the asymptotic behavior of the magnitudes of the real and imaginary parts.
plot(z,real(H),z,imag(H)) grid on hold on M = sqrt(real(H).^2 + imag(H).^2); plot(z,M,'--') legend('$J_0(z)$', '$Y_0(z)$', '$\sqrt{J_0^2 (z) + Y_0^2 (z)}$','interpreter','latex')
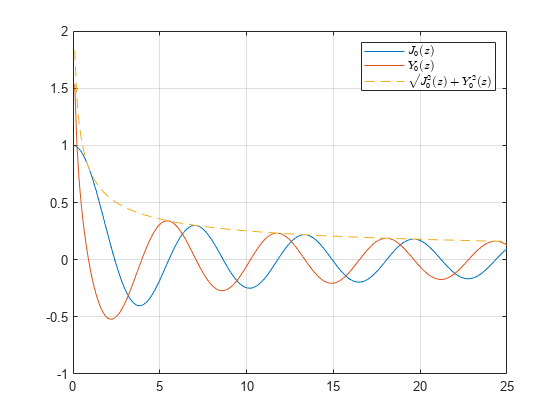
Exponentially Scaled Hankel Function
Calculate the exponentially scaled Hankel function on the complex plane and compare it to the unscaled function.
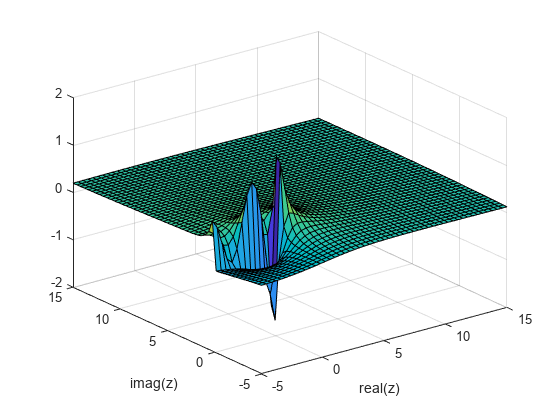
Calculate the unscaled Hankel function of the second order on the complex plane. When z has a large positive imaginary part, the value of the function quickly diverges. This phenomenon limits the range of computable values.
k = 2; nu = 1; x = -5:0.4:15; y = x'; z = x + 1i*y; scaled = 1; H = besselh(nu,k,z); surf(x,y,imag(H)) xlabel('real(z)') ylabel('imag(z)')
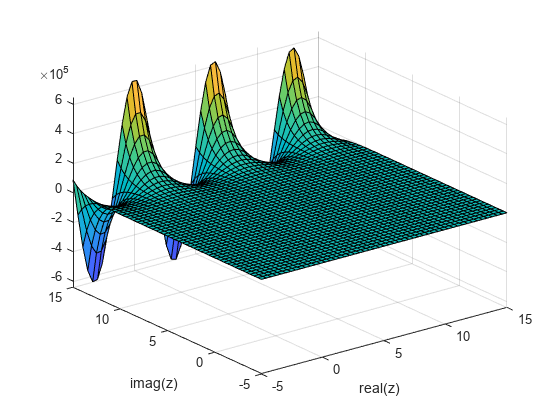
Now, calculate on the complex plane and compare it to the unscaled function. The scaled function increases the range of computable values by avoiding overflow and loss of accuracy when z has a large positive imaginary part.
Hs = besselh(nu,k,z,scaled); surf(x,y,imag(Hs)) xlabel('real(z)') ylabel('imag(z)')
Input Arguments
nu — Equation order
scalar | vector | matrix | multidimensional array
Equation order, specified as a scalar, vector, matrix, or multidimensional array.
nu specifies the order of the Hankel function. nu and Z must be the
same size, or one of them can be scalar.
Example: besselh(3,Z)
Data Types: single | double
K — Kind of Hankel function
1 (default) | 2
Kind of Hankel function, specified as 1 or 2.
If
K = 1, thenbesselhcomputes the Hankel function of the first kind .If
K = 2, thenbesselhcomputes the Hankel function of the second kind .
Example: besselh(nu,2,Z)
Z — Functional domain
scalar | vector | matrix | multidimensional array
Functional domain, specified as a scalar, vector, matrix, or multidimensional array.
nu and Z must be the same size, or one of them
can be scalar.
Example: besselh(nu,[1-1i 1+0i 1+1i])
Data Types: single | double
Complex Number Support: Yes
scale — Toggle to scale function
0 (default) | 1
Toggle to scale function, specified as one of these values:
0(default) — No scaling1— Scale the output ofbesselh, depending on the value ofK:If
K = 1, then scale the Hankel function of the first kind by .If
K = 2, then scale Hankel function of the second kind by .
On the complex plane, overflows when
imag(Z)is large and negative. Similarly, overflows whenimag(Z)is large and positive. Exponentially scaling the output ofbesselhis useful in these two cases since the function otherwise quickly loses accuracy or overflows the limits of double precision.
Example: besselh(nu,K,Z,1)
More About
Hankel Functions and Bessel’s Equation
This differential equation, where ν is a real constant, is called Bessel's equation:
Its solutions are known as Bessel functions.
The Bessel functions of the first kind, denoted Jν(z) and J–ν(z), form a fundamental set of solutions of Bessel's equation for noninteger ν. The Bessel functions of the second kind, denoted Yν(z), form a second solution of Bessel's equation—linearly independent of Jν(z)—defined by
The Bessel functions of the third kind, also called
Hankel functions of the first and second kind, are defined by linear
combinations of the Bessel functions, where Jν(z) is besselj, and Yν(z) is bessely:
References
[1] Abramowitz, M., and I.A. Stegun. Handbook of Mathematical Functions. National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Always returns a complex result.
Strict single-precision calculations are not supported. In the generated code, single-precision inputs produce single-precision outputs. However, variables inside the function might be double-precision.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
Always returns a complex result.
Strict single-precision calculations are not supported. In the generated code, single-precision inputs produce single-precision outputs. However, variables inside the function might be double-precision.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)