colamd
Column approximate minimum degree permutation
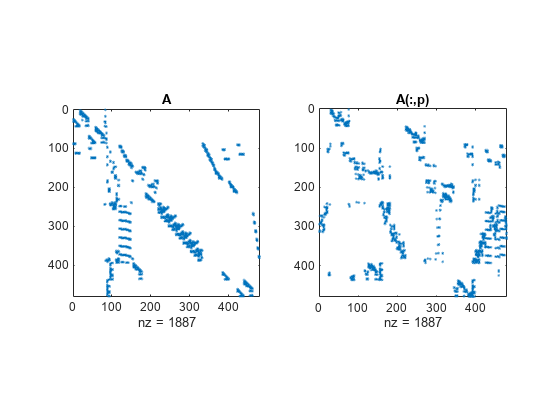
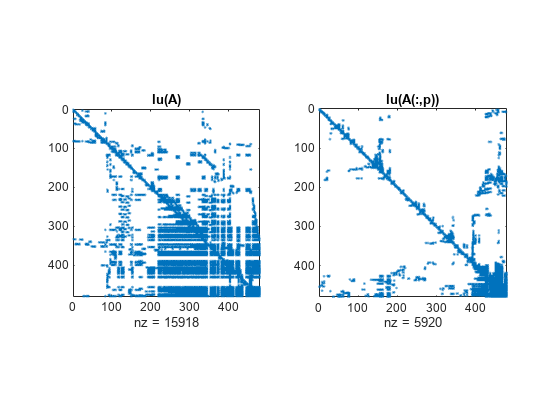
Description
Examples
Input Arguments
Output Arguments
References
[1] Davis, Timothy A., John R. Gilbert, Stefan I. Larimore, and Esmond G. Ng. “Algorithm 836: COLAMD, a Column Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 377–380. https://doi.org/10.1145/1024074.1024080.
Extended Capabilities
Version History
Introduced before R2006a