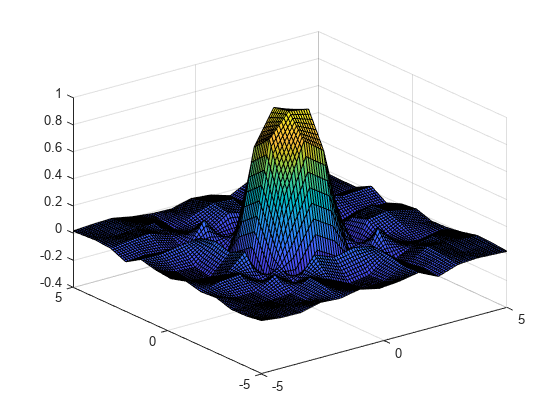
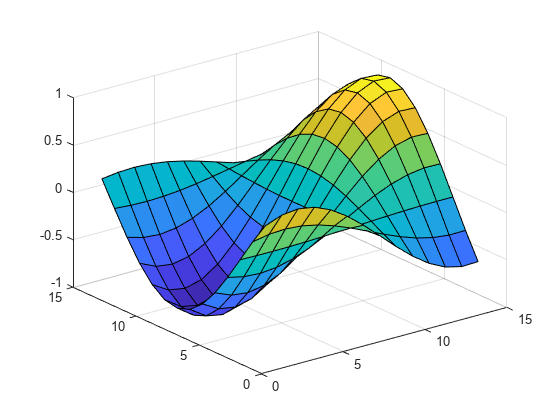
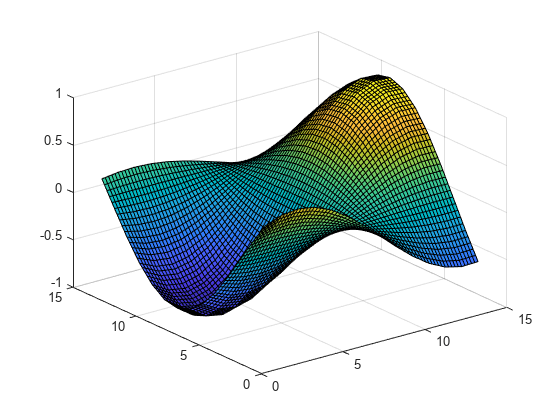
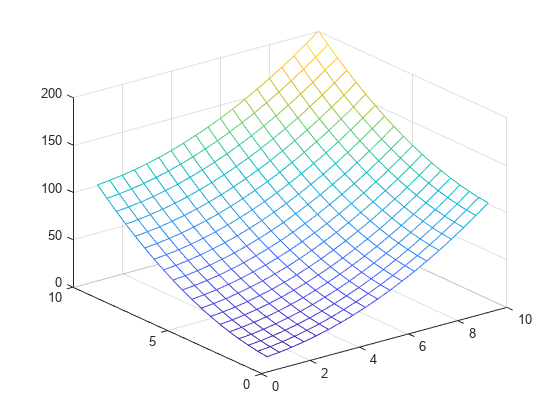
griddedInterpolant
Gridded data interpolation
Description
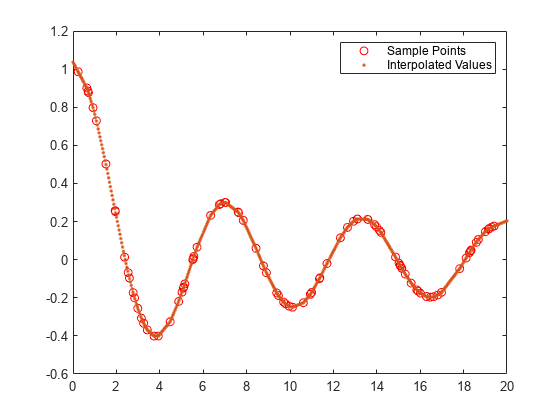
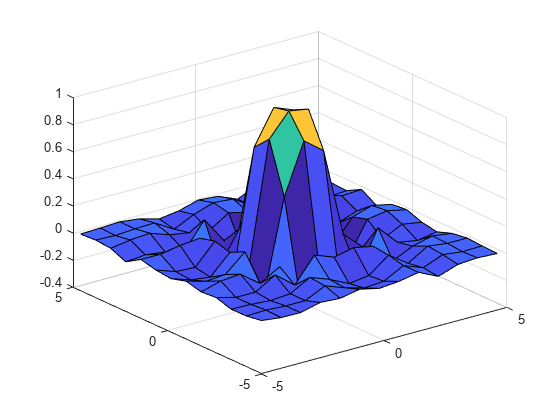
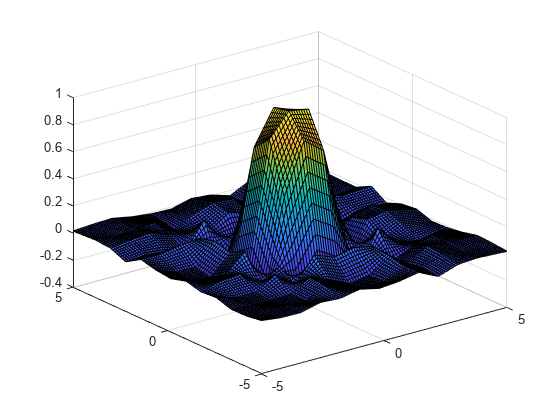
Use griddedInterpolant to perform interpolation on a 1-D,
2-D, 3-D, or N-D gridded data set.
griddedInterpolant returns the interpolant
F for the given data set. You can evaluate F at a
set of query points, such as (xq,yq) in 2-D, to produce interpolated
values vq = F(xq,yq).
Use scatteredInterpolant to perform
interpolation with scattered data.
Creation
Syntax
Description
F = griddedInterpolant
F = griddedInterpolant(X1,X2,...,Xn,V)n-dimensional arrays X1,X2,...,Xn. The
V array contains the sample values associated with the
point locations in X1,X2,...,Xn. Each of the arrays
X1,X2,...,Xn must be the same size as
V.
F = griddedInterpolant(V)griddedInterpolant defines the grid as a
set of points whose spacing is 1 and range is
[1, size(V,i)] in the
ith dimension. Use this syntax when you want to conserve
memory and are not concerned about the absolute distances between points.
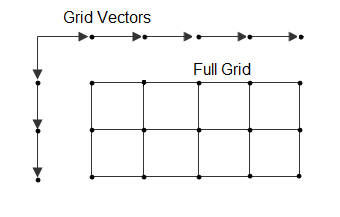
F = griddedInterpolant(gridVecs,V)gridVecs that contains
n
grid vectors to
describe an n-dimensional grid of sample points. Use this
syntax when you want to use a specific grid and also conserve memory.
F = griddedInterpolant(___,Method)'linear',
'nearest', 'next',
'previous', 'pchip',
'cubic', 'makima', or
'spline'. You can specify Method as
the last input argument in any of the previous syntaxes.
F = griddedInterpolant(___,Method,ExtrapolationMethod)griddedInterpolant uses
ExtrapolationMethod to estimate the value when your query
points fall outside the domain of your sample points.
Input Arguments
Properties
Usage
Description
Use griddedInterpolant to create the interpolant,
F. Then you can evaluate F at specific
query points using any of the following syntaxes:
Vq = F(Xq) specifies the query points in the matrix
Xq. Each row of Xq contains the
coordinates of a query point.
Vq = F(xq1,xq2,...,xqn) specifies the query points
xq1,xq2,...,xqn as column vectors of length
m, representing m points scattered in
n-dimensional space.
Vq = F(Xq1,Xq2,...,Xqn) specifies the query points using
the n-dimensional arrays Xq1,Xq2,...,Xqn,
which define a full grid of
points.
Vq = F({xgq1,xgq2,...,xgqn}) specifies the query points
as grid vectors. Use
this syntax to conserve memory when you want to query a large grid of
points.
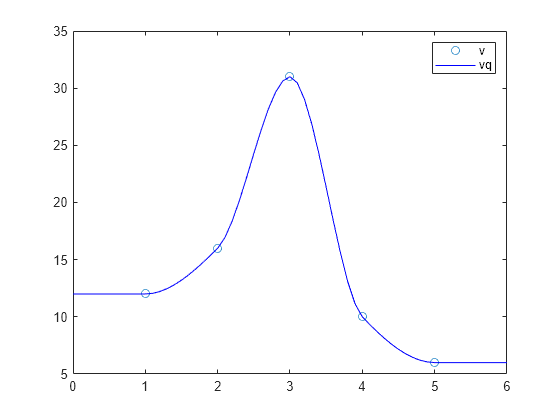
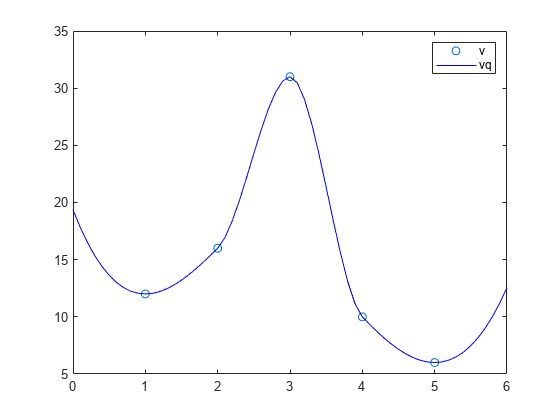
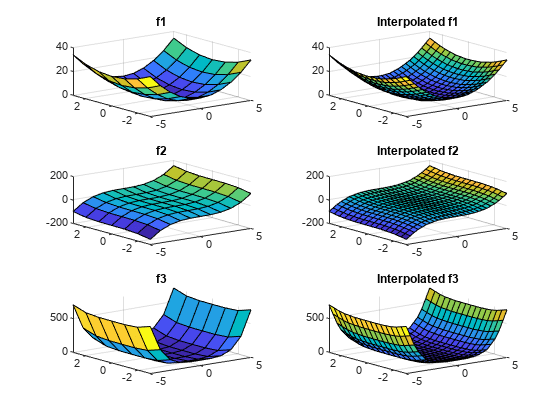
Examples
More About
Tips
It is quicker to evaluate a
griddedInterpolantobjectFat many different sets of query points than it is to compute the interpolations separately usinginterp1,interp2,interp3, orinterpn. For example:% Fast to create interpolant F and evaluate multiple times F = griddedInterpolant(X1,X2,V) v1 = F(Xq1) v2 = F(Xq2) % Slower to compute interpolations separately using interp2 v1 = interp2(X1,X2,V,Xq1) v2 = interp2(X1,X2,V,Xq2)
Extended Capabilities
Version History
Introduced in R2011bSee Also
scatteredInterpolant | interp1 | interp2 | interp3 | interpn | ndgrid | meshgrid | fillmissing | filloutliers