mldivide, \
Solve systems of linear equations Ax = B for x
Syntax
Description
x = A\BA*x =
B. The matrices A and
B must have the same number of
rows. MATLAB® displays a warning message if
A is badly scaled or nearly
singular, but performs the calculation regardless.
If
Ais a scalar, thenA\Bis equivalent toA.\B.If
Ais a squaren-by-nmatrix andBis a matrix withnrows, thenx = A\Bis a solution to the equationA*x = B, if it exists.If
Ais a rectangularm-by-nmatrix withm ~= n, andBis a matrix withmrows, thenA\Breturns a least-squares solution to the system of equationsA*x= B.xmay not be the minimum-norm solution.
Examples
Input Arguments
Output Arguments
Tips
The operators
/and\are related to each other by the equationB/A = (A'\B')'.If
Ais a square matrix, thenA\Bis roughly equal toinv(A)*B, but MATLAB processesA\Bdifferently and more robustly.If the rank of
Ais less than the number of columns inA, thenx = A\Bis not necessarily the minimum-norm solution. You can compute the minimum-norm least-squares solution usingx =orlsqminnorm(A,B)x =.pinv(A)*BUse
decompositionobjects to efficiently solve a linear system multiple times with different right-hand sides.decompositionobjects are well-suited to solving problems that require repeated solutions, since the decomposition of the coefficient matrix does not need to be performed multiple times.
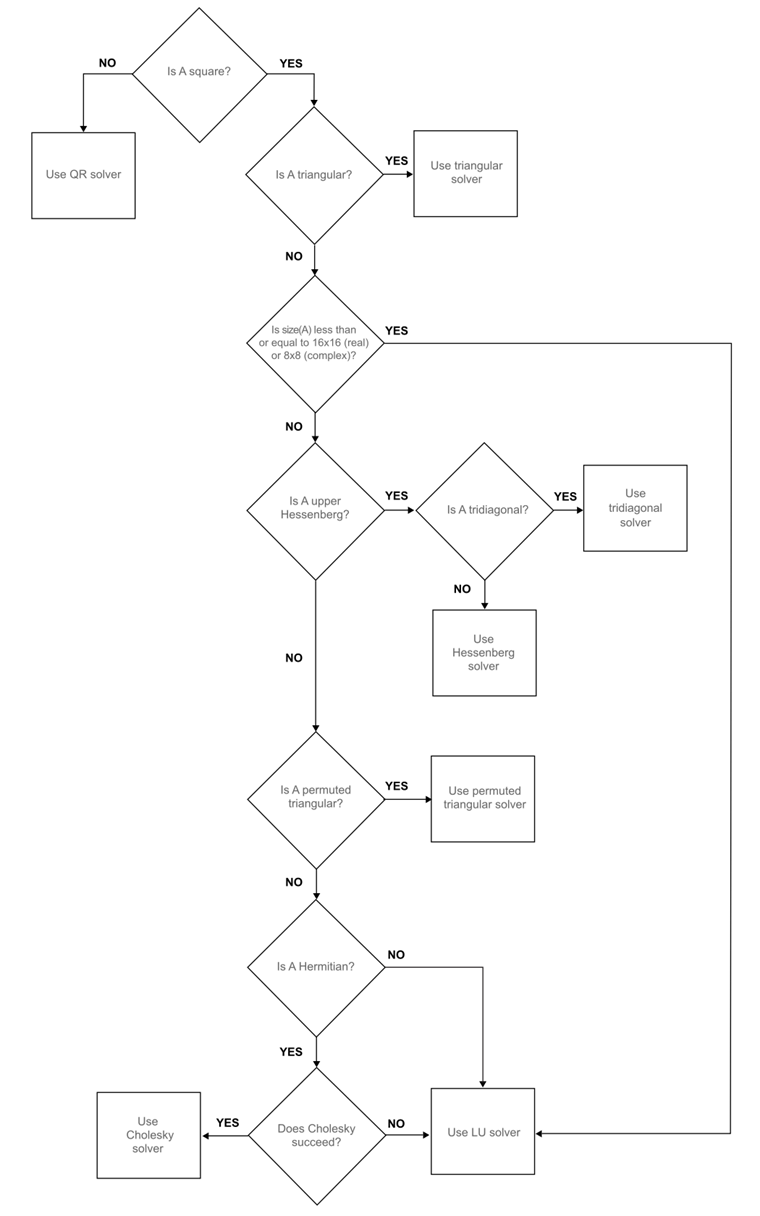
Algorithms
References
[1] Gilbert, John R., and Tim Peierls. “Sparse Partial Pivoting in Time Proportional to Arithmetic Operations.” SIAM Journal on Scientific and Statistical Computing 9, no. 5 (September 1988): 862–874. https://doi.org/10.1137/0909058.
[2] Anderson, E., ed. LAPACK Users’ Guide. 3rd ed. Software, Environments, Tools. Philadelphia: Society for Industrial and Applied Mathematics, 1999. https://doi.org/10.1137/1.9780898719604.
[3] Davis, Timothy A. "Algorithm 832: UMFPACK V4.3 – an unsymmetric-pattern multifrontal method." ACM Transactions on Mathematical Software 30, no. 2 (June 2004): 196–199. https://doi.org/10.1145/992200.992206.
[4] Duff, Iain S. “MA57---a Code for the Solution of Sparse Symmetric Definite and Indefinite Systems.” ACM Transactions on Mathematical Software 30, no. 2 (June 2004): 118–144. https://doi.org/10.1145/992200.992202.
[5] Davis, Timothy A., John R. Gilbert, Stefan I. Larimore, and Esmond G. Ng. “Algorithm 836: COLAMD, a Column Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 377–380. https://doi.org/10.1145/1024074.1024080.
[6] Amestoy, Patrick R., Timothy A. Davis, and Iain S. Duff. “Algorithm 837: AMD, an Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 381–388. https://doi.org/10.1145/1024074.1024081.
[7] Chen, Yanqing, Timothy A. Davis, William W. Hager, and Sivasankaran Rajamanickam. “Algorithm 887: CHOLMOD, Supernodal Sparse Cholesky Factorization and Update/Downdate.” ACM Transactions on Mathematical Software 35, no. 3 (October 2008): 1–14. https://doi.org/10.1145/1391989.1391995.
[8] Davis, Timothy A. “Algorithm 915, SuiteSparseQR: Multifrontal Multithreaded Rank-Revealing Sparse QR Factorization.” ACM Transactions on Mathematical Software 38, no. 1 (November 2011): 1–22. https://doi.org/10.1145/2049662.2049670.