ode15s
Solve stiff differential equations and DAEs — variable order method
Syntax
Description
[,
where t,y] =
ode15s(odefun,tspan,y0)tspan = [t0 tf], integrates the system of
differential equations from t0 to tf with
initial conditions y0. Each row in the solution
array y corresponds to a value returned in column
vector t.
All MATLAB® ODE solvers can solve systems of equations of
the form ,
or problems that involve a mass matrix, .
The solvers all use similar syntaxes. The ode23s solver
only can solve problems with a mass matrix if the mass matrix is constant. ode15s and ode23t can
solve problems with a mass matrix that is singular, known as differential-algebraic
equations (DAEs). Specify the mass matrix using the Mass option
of odeset.
[ additionally
finds where functions of (t,y),
called event functions, are zero. In the output, t,y,te,ye,ie]
= ode15s(odefun,tspan,y0,options)te is
the time of the event, ye is the solution at the
time of the event, and ie is the index of the triggered
event.
For each event function, specify whether the integration is
to terminate at a zero and whether the direction of the zero crossing
matters. Do this by setting the 'Events' property
to a function, such as myEventFcn or @myEventFcn,
and creating a corresponding function: [value,isterminal,direction]
= myEventFcn(t,y).
For more information, see ODE Event Location.
Examples
ODE with Single Solution Component
Simple ODEs that have a single solution component can be specified as an anonymous function in the call to the solver. The anonymous function must accept two inputs (t,y), even if one of the inputs is not used in the function.
Solve the ODE
Specify a time interval of [0 2] and the initial condition y0 = 1.
tspan = [0 2]; y0 = 1; [t,y] = ode15s(@(t,y) -10*t, tspan, y0);
Plot the solution.
plot(t,y,'-o')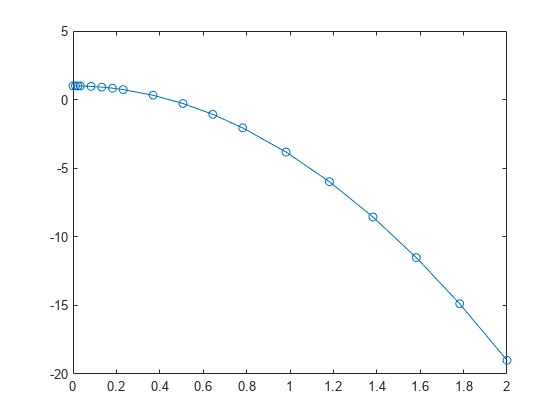
Solve Stiff ODE
An example of a stiff system of equations is the van der Pol equations in relaxation oscillation. The limit cycle has regions where the solution components change slowly and the problem is quite stiff, alternating with regions of very sharp change where it is not stiff.
The system of equations is:
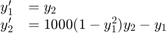
The initial conditions are 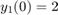 and
and 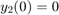 . The function
. The function vdp1000 ships with MATLAB® and encodes the equations.
function dydt = vdp1000(t,y) %VDP1000 Evaluate the van der Pol ODEs for mu = 1000. % % See also ODE15S, ODE23S, ODE23T, ODE23TB. % Jacek Kierzenka and Lawrence F. Shampine % Copyright 1984-2014 The MathWorks, Inc. dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];
Solving this system using ode45 with the default relative and absolute error tolerances (1e-3 and 1e-6, respectively) is extremely slow, requiring several minutes to solve and plot the solution. ode45 requires millions of time steps to complete the integration, due to the areas of stiffness where it struggles to meet the tolerances.
This is a plot of the solution obtained by ode45, which takes a long time to compute. Notice the enormous number of time steps required to pass through areas of stiffness.
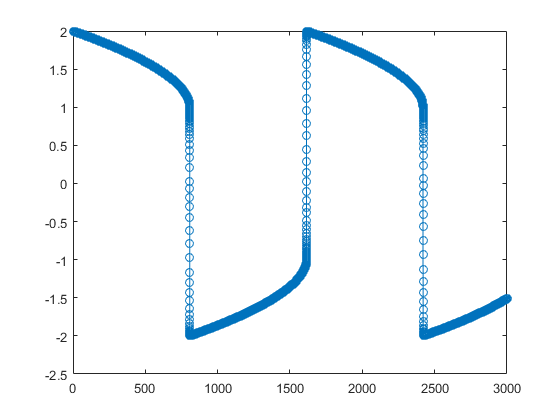
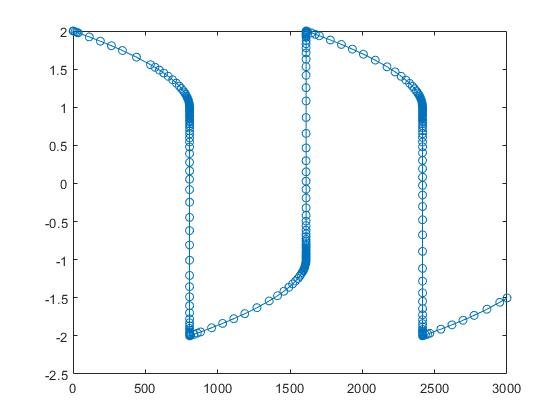
Solve the stiff system using the ode15s solver, and then plot the first column of the solution y against the time points t. The ode15s solver passes through stiff areas with far fewer steps than ode45.
[t,y] = ode15s(@vdp1000,[0 3000],[2 0]);
plot(t,y(:,1),'-o')
Pass Extra Parameters to ODE Function
ode15s only works with functions that use two input arguments, t and y. However, you can pass in extra parameters by defining them outside the function and passing them in when you specify the function handle.
Solve the ODE
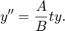
Rewriting the equation as a first-order system yields
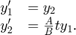
odefcn.m represents this system of equations as a function that accepts four input arguments: t, y, A, and B.
function dydt = odefcn(t,y,A,B)
dydt = zeros(2,1);
dydt(1) = y(2);
dydt(2) = (A/B)*t.*y(1);
Solve the ODE using ode15s. Specify the function handle such that it passes in the predefined values for A and B to odefcn.
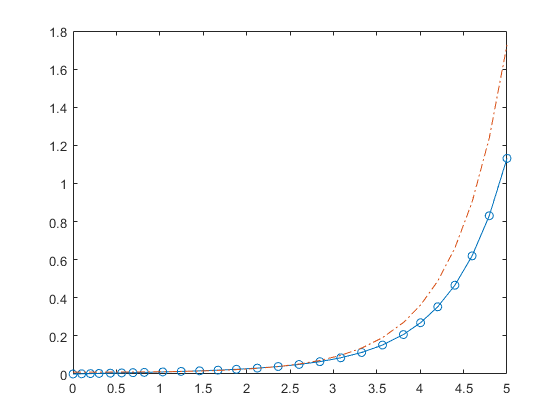
A = 1; B = 2; tspan = [0 5]; y0 = [0 0.01]; [t,y] = ode15s(@(t,y) odefcn(t,y,A,B), tspan, y0);
Plot the results.
plot(t,y(:,1),'-o',t,y(:,2),'-.')
Compare Stiff ODE Solvers
The ode15s solver is a good first choice for most stiff problems. However, the other stiff solvers might be more efficient for certain types of problems. This example solves a stiff test equation using all four stiff ODE solvers.
Consider the test equation
The equation becomes increasingly stiff as the magnitude of increases. Use and the initial condition over the time interval [0 0.5]. With these values, the problem is stiff enough that ode45 and ode23 struggle to integrate the equation. Also, use odeset to pass in the constant Jacobian and turn on the display of solver statistics.
lambda = 1e9; y0 = 1; tspan = [0 0.5]; opts = odeset('Jacobian',-lambda,'Stats','on');
Solve the equation with ode15s, ode23s, ode23t, and ode23tb. Make subplots for comparison.
subplot(2,2,1) tic, ode15s(@(t,y) -lambda*y, tspan, y0, opts), toc
104 successful steps 1 failed attempts 212 function evaluations 0 partial derivatives 21 LU decompositions 210 solutions of linear systems Elapsed time is 1.117982 seconds.
title('ode15s')
subplot(2,2,2)
tic, ode23s(@(t,y) -lambda*y, tspan, y0, opts), toc63 successful steps 0 failed attempts 191 function evaluations 0 partial derivatives 63 LU decompositions 189 solutions of linear systems Elapsed time is 0.179014 seconds.
title('ode23s')
subplot(2,2,3)
tic, ode23t(@(t,y) -lambda*y, tspan, y0, opts), toc95 successful steps 0 failed attempts 125 function evaluations 0 partial derivatives 28 LU decompositions 123 solutions of linear systems Elapsed time is 0.233392 seconds.
title('ode23t')
subplot(2,2,4)
tic, ode23tb(@(t,y) -lambda*y, tspan, y0, opts), toc71 successful steps 0 failed attempts 167 function evaluations 0 partial derivatives 23 LU decompositions 236 solutions of linear systems Elapsed time is 0.234603 seconds.
title('ode23tb')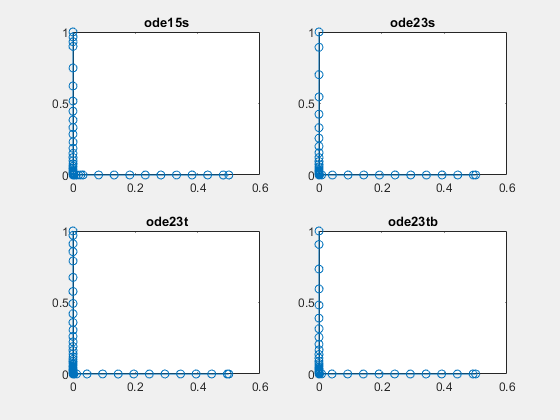
The stiff solvers all perform well, but ode23s completes the integration with the fewest steps and runs the fastest for this particular problem. Since the constant Jacobian is specified, none of the solvers need to calculate partial derivatives to compute the solution. Specifying the Jacobian benefits ode23s the most since it normally evaluates the Jacobian in every step.
For general stiff problems, the performance of the stiff solvers varies depending on the format of the problem and specified options. Providing the Jacobian matrix or sparsity pattern always improves solver efficiency for stiff problems. But since the stiff solvers use the Jacobian differently, the improvement can vary significantly. Practically speaking, if a system of equations is very large or needs to be solved many times, then it is worthwhile to investigate the performance of the different solvers to minimize execution time.
Evaluate and Extend Solution Structure
The van der Pol equation is a second order ODE
Solve the van der Pol equation with using ode15s. The function vdp1000.m ships with MATLAB® and encodes the equations. Specify a single output to return a structure containing information about the solution, such as the solver and evaluation points.
tspan = [0 3000]; y0 = [2 0]; sol = ode15s(@vdp1000,tspan,y0)
sol = struct with fields:
solver: 'ode15s'
extdata: [1x1 struct]
x: [0 1.4606e-05 2.9212e-05 4.3818e-05 1.1010e-04 1.7639e-04 2.4267e-04 3.0896e-04 4.5006e-04 5.9116e-04 7.3226e-04 8.7336e-04 0.0010 0.0012 0.0013 0.0015 0.0017 0.0018 0.0021 0.0024 0.0027 0.0030 0.0033 0.0044 0.0055 0.0066 ... ] (1x592 double)
y: [2x592 double]
stats: [1x1 struct]
idata: [1x1 struct]
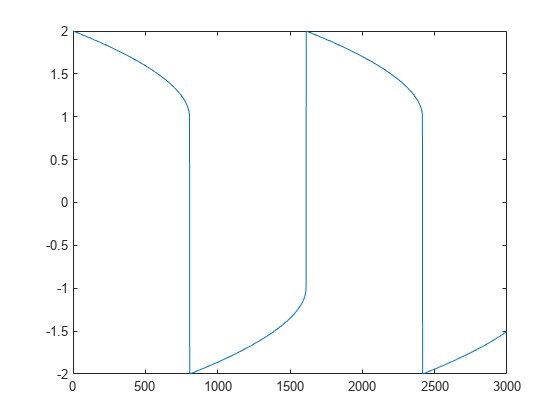
Use linspace to generate 2500 points in the interval [0 3000]. Evaluate the first component of the solution at these points using deval.
x = linspace(0,3000,2500); y = deval(sol,x,1);
Plot the solution.
plot(x,y)
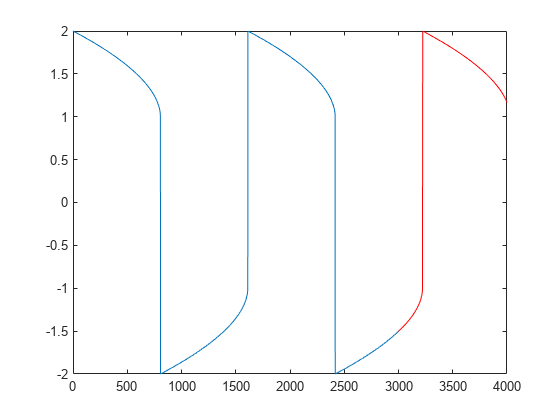
Extend the solution to using odextend and add the result to the original plot.
tf = 4000; sol_new = odextend(sol,@vdp1000,tf); x = linspace(3000,tf,350); y = deval(sol_new,x,1); hold on plot(x,y,'r')
Solve Robertson Problem as Semi-Explicit Differential Algebraic Equations (DAEs)
This example reformulates a system of ODEs as a system of differential algebraic equations (DAEs). The Robertson problem found in hb1ode.m is a classic test problem for programs that solve stiff ODEs. The system of equations is
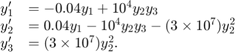
hb1ode solves this system of ODEs to steady state with the initial conditions 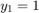 ,
, 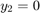 , and
, and 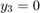 . But the equations also satisfy a linear conservation law,
. But the equations also satisfy a linear conservation law,
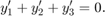
In terms of the solution and initial conditions, the conservation law is
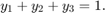
The system of equations can be rewritten as a system of DAEs by using the conservation law to determine the state of 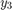 . This reformulates the problem as the DAE system
. This reformulates the problem as the DAE system
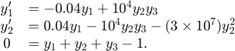
The differential index of this system is 1, since only a single derivative of 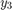 is required to make this a system of ODEs. Therefore, no further transformations are required before solving the system.
is required to make this a system of ODEs. Therefore, no further transformations are required before solving the system.
The function robertsdae encodes this DAE system. Save robertsdae.m in your current folder to run the example.
function out = robertsdae(t,y)
out = [-0.04*y(1) + 1e4*y(2).*y(3)
0.04*y(1) - 1e4*y(2).*y(3) - 3e7*y(2).^2
y(1) + y(2) + y(3) - 1 ];
The full example code for this formulation of the Robertson problem is available in hb1dae.m.
Solve the DAE system using ode15s. Consistent initial conditions for y0 are obvious based on the conservation law. Use odeset to set the options:
Use a constant mass matrix to represent the left hand side of the system of equations.
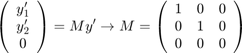
Set the relative error tolerance to
1e-4.Use an absolute tolerance of
1e-10for the second solution component, since the scale varies dramatically from the other components.Leave the
'MassSingular'option at its default value'maybe'to test the automatic detection of a DAE.
y0 = [1; 0; 0]; tspan = [0 4*logspace(-6,6)]; M = [1 0 0; 0 1 0; 0 0 0]; options = odeset('Mass',M,'RelTol',1e-4,'AbsTol',[1e-6 1e-10 1e-6]); [t,y] = ode15s(@robertsdae,tspan,y0,options);
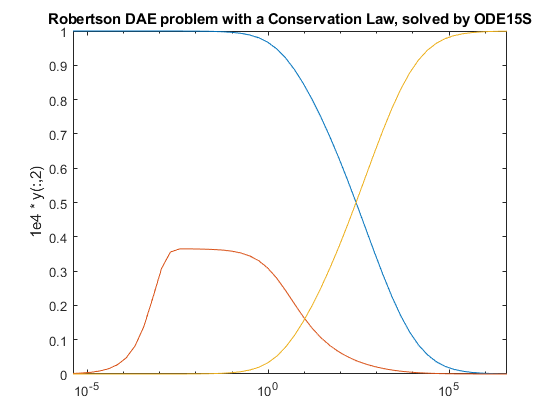
Plot the solution.
y(:,2) = 1e4*y(:,2); semilogx(t,y); ylabel('1e4 * y(:,2)'); title('Robertson DAE problem with a Conservation Law, solved by ODE15S');
Input Arguments
odefun — Functions to solve
function handle
Functions to solve, specified as a function handle that defines the functions to be integrated.
The function dydt = odefun(t,y), for a scalar t and a
column vector y, must return a column vector
dydt of data type single or
double that corresponds to . odefun must accept both input arguments
t and y, even if one of the arguments is
not used in the function.
For example, to solve , use the function:
function dydt = odefun(t,y) dydt = 5*y-3; end
For a system of equations, the output of odefun is a vector. Each element
in the vector is the computed value of the right side of one equation. For example,
consider the system of two equations
A function that calculates the value of the right side of each equation at each time step is
function dydt = odefun(t,y) dydt = zeros(2,1); dydt(1) = y(1)+2*y(2); dydt(2) = 3*y(1)+2*y(2); end
For information on how to provide additional parameters to the
function odefun, see Parameterizing Functions.
Example: @myFcn
Data Types: function_handle
tspan — Interval of integration
vector
Interval of integration, specified as a vector. At a minimum, tspan must be
a two-element vector [t0 tf] specifying the initial and final
times. To obtain solutions at specific times between t0 and
tf, use a longer vector of the form
[t0,t1,t2,...,tf]. The elements in tspan
must be all increasing or all decreasing.
The solver imposes the initial conditions given by y0 at the initial time
tspan(1), and then integrates from
tspan(1) to tspan(end):
If
tspanhas two elements[t0 tf], then the solver returns the solution evaluated at each internal integration step within the interval.If
tspanhas more than two elements[t0,t1,t2,...,tf], then the solver returns the solution evaluated at the given points. However, the solver does not step precisely to each point specified intspan. Instead, the solver uses its own internal steps to compute the solution, and then evaluates the solution at the requested points intspan. The solutions produced at the specified points are of the same order of accuracy as the solutions computed at each internal step.Specifying several intermediate points has little effect on the efficiency of computation, but can affect memory management for large systems.
The values of tspan are used by the solver to calculate
suitable values for InitialStep and MaxStep:
If
tspancontains several intermediate points[t0,t1,t2,...,tf], then the specified points give an indication of the scale for the problem, which can affect the value ofInitialStepused by the solver. Therefore, the solution obtained by the solver might be different depending on whether you specifytspanas a two-element vector or as a vector with intermediate points.The initial and final values in
tspanare used to calculate the maximum step sizeMaxStep. Therefore, changing the initial or final values intspancan cause the solver to use a different step sequence, which might change the solution.
Example: [1 10]
Example: [1
3 5 7 9 10]
Data Types: single | double
y0 — Initial conditions
vector
Initial conditions, specified as a vector. y0 must
be the same length as the vector output of odefun,
so that y0 contains an initial condition for each
equation defined in odefun.
Data Types: single | double
options — Option structure
structure array
Option structure, specified as a structure array. Use the odeset function to create or modify the options
structure. See Summary of ODE Options for a list of
the options compatible with each solver.
Example: options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot) specifies
a relative error tolerance of 1e-5, turns on the
display of solver statistics, and specifies the output function @odeplot to
plot the solution as it is computed.
Data Types: struct
Output Arguments
t — Evaluation points
column vector
Evaluation points, returned as a column vector.
If
tspancontains two elements[t0 tf], thentcontains the internal evaluation points used to perform the integration.If
tspancontains more than two elements, thentis the same astspan.
y — Solutions
array
Solutions, returned as an array. Each row in y corresponds
to the solution at the value returned in the corresponding row of t.
te — Time of events
column vector
Time of events, returned as a column vector. The event times
in te correspond to the solutions returned in ye,
and ie specifies which event occurred.
ye — Solution at time of events
array
Solution at time of events, returned as an array. The event
times in te correspond to the solutions returned
in ye, and ie specifies which
event occurred.
ie — Index of triggered event function
column vector
Index of triggered event function, returned as a column vector. The event times in
te correspond to the solutions returned in
ye, and ie specifies which event
occurred.
sol — Structure for evaluation
structure array
Structure for evaluation, returned as a structure array. Use this structure with the deval function to evaluate the solution at any point in the interval
[t0 tf]. The sol structure array always
includes these fields:
| Structure Field | Description |
|---|---|
| Row vector of the steps chosen by the solver. |
| Solutions. Each column |
| Solver name. |
Additionally, if you specify the Events option of
odeset and events are detected, then sol
also includes these fields:
| Structure Field | Description |
|---|---|
| Points when events occurred.
|
| Solutions that correspond to events in
|
| Indices into the vector returned by the function
specified in the |
Algorithms
ode15s is a variable-step, variable-order
(VSVO) solver based on the numerical differentiation formulas (NDFs)
of orders 1 to 5. Optionally, it can use the backward differentiation
formulas (BDFs, also known as Gear's method) that are usually less
efficient. Like ode113, ode15s is
a multistep solver. Use ode15s if ode45 fails
or is very inefficient and you suspect that the problem is stiff,
or when solving a differential-algebraic equation (DAE) [1], [2].
References
[1] Shampine, L. F. and M. W. Reichelt, “The MATLAB ODE Suite,” SIAM Journal on Scientific Computing, Vol. 18, 1997, pp. 1–22.
[2] Shampine, L. F., M. W. Reichelt, and J.A. Kierzenka, “Solving Index-1 DAEs in MATLAB and Simulink,” SIAM Review, Vol. 41, 1999, pp. 538–552.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
odesetinputsJPatternandMvPatternmust be passed as function handles that return either a sparse or full matrix.odesetinputsMassandJacobianmust be passed as full matrices or as functions that return full or sparse matrices. To pass a sparse matrix, you must pass a function.All
odesetoption arguments must be constant.Variable-sizing support and dynamic memory allocation must be enabled.
Input types must be homogenous – all double or all single.
You must provide at least two output arguments,
tandy.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)