pchip
Piecewise Cubic Hermite Interpolating Polynomial (PCHIP)
Description
p = pchip(x,y,xq)p corresponding
to the query points in xq. The values of p are
determined by shape-preserving piecewise cubic
interpolation of x and y.
Examples
Data Interpolation with spline, pchip, and makima
Compare the interpolation results produced by spline, pchip, and makima for two different data sets. These functions all perform different forms of piecewise cubic Hermite interpolation. Each function differs in how it computes the slopes of the interpolant, leading to different behaviors when the underlying data has flat areas or undulations.
Compare the interpolation results on sample data that connects flat regions. Create vectors of x values, function values at those points y, and query points xq. Compute interpolations at the query points using spline, pchip, and makima. Plot the interpolated function values at the query points for comparison.
x = -3:3; y = [-1 -1 -1 0 1 1 1]; xq1 = -3:.01:3; p = pchip(x,y,xq1); s = spline(x,y,xq1); m = makima(x,y,xq1); plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--') legend('Sample Points','pchip','spline','makima','Location','SouthEast')
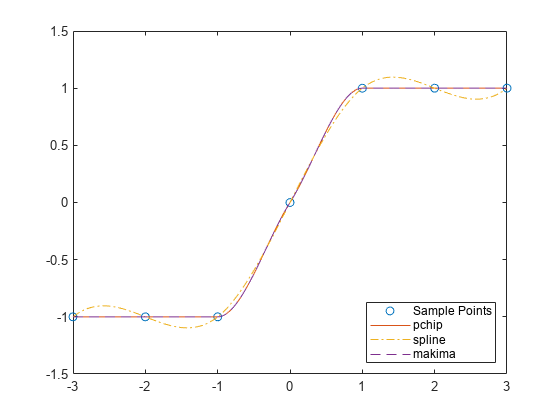
In this case, pchip and makima have similar behavior in that they avoid overshoots and can accurately connect the flat regions.
Perform a second comparison using an oscillatory sample function.
x = 0:15; y = besselj(1,x); xq2 = 0:0.01:15; p = pchip(x,y,xq2); s = spline(x,y,xq2); m = makima(x,y,xq2); plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--') legend('Sample Points','pchip','spline','makima')
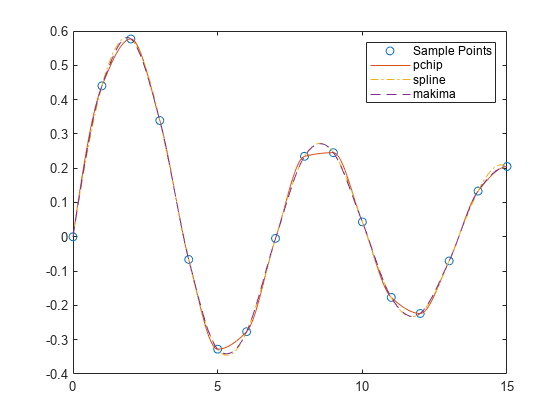
When the underlying function is oscillatory, spline and makima capture the movement between points better than pchip, which is aggressively flattened near local extrema.
Interpolation with Piecewise Polynomial Structure
Create vectors for the x values and function values y, and then use pchip to construct a piecewise polynomial structure.
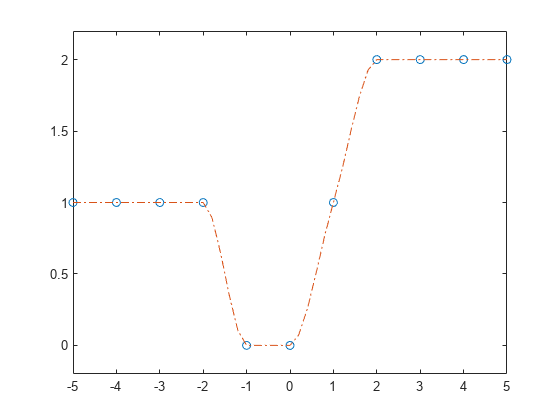
x = -5:5; y = [1 1 1 1 0 0 1 2 2 2 2]; p = pchip(x,y);
Use the structure with ppval to evaluate the interpolation at several query points. Plot the results.
xq = -5:0.2:5; pp = ppval(p,xq); plot(x,y,'o',xq,pp,'-.') ylim([-0.2 2.2])
Input Arguments
x — Sample points
vector
Sample points, specified as a vector. The vector x specifies
the points at which the data y is given. The elements
of x must be unique.
Data Types: single | double
y — Function values at sample points
vector | matrix | array
Function values at sample points, specified as a numeric vector,
matrix, or array. x and y must
have the same length.
If y is a matrix or array, then the values
in the last dimension, y(:,...,:,j), are taken
as the values to match with x. In that case, the
last dimension of y must be the same length as x.
Data Types: single | double
xq — Query points
scalar | vector | matrix | array
Query points, specified as a scalar, vector, matrix, or array. The points
specified in xq are the x-coordinates
for the interpolated function values yq computed by
pchip.
Data Types: single | double
Output Arguments
p — Interpolated values at query points
scalar | vector | matrix | array
Interpolated values at query points, returned as a scalar, vector, matrix,
or array. The size of p is related to the sizes of
y and xq:
If
yis a vector, thenphas the same size asxq.If
yis an array of sizeNy = size(y), then these conditions apply:If
xqis a scalar or vector, thensize(p)returns[Ny(1:end-1) length(xq)].If
xqis an array, thensize(p)returns[Ny(1:end-1) size(xq).
pp — Piecewise polynomial
structure
Piecewise polynomial, returned as a structure. Use this structure
with the ppval function to
evaluate the interpolating polynomials at one or more query points.
The structure has these fields.
| Field | Description |
|---|---|
form |
|
breaks | Vector of length |
coefs |
|
pieces | Number of pieces, |
order | Order of the polynomials |
dim | Dimensionality of target |
Since the polynomial coefficients in coefs are
local coefficients for each interval, you must subtract the lower
endpoint of the corresponding knot interval to use the coefficients
in a conventional polynomial equation. In other words, for the coefficients [a,b,c,d] on
the interval [x1,x2], the corresponding polynomial
is
More About
Shape-Preserving Piecewise Cubic Interpolation
pchip interpolates using
a piecewise cubic polynomial with
these properties:
On each subinterval , the polynomial is a cubic Hermite interpolating polynomial for the given data points with specified derivatives (slopes) at the interpolation points.
interpolates y, that is, , and the first derivative is continuous. The second derivative is probably not continuous so jumps at the are possible.
The cubic interpolant is shape preserving. The slopes at the are chosen in such a way that preserves the shape of the data and respects monotonicity. Therefore, on intervals where the data is monotonic, so is , and at points where the data has a local extremum, so does .
Note
If y is a matrix, satisfies these properties for each row of y.
Tips
splineconstructs in almost the same waypchipconstructs . However,splinechooses the slopes at the differently, namely to make even continuous. This difference has several effects:splineproduces a smoother result, such that is continuous.splineproduces a more accurate result if the data consists of values of a smooth function.pchiphas no overshoots and less oscillation if the data is not smooth.pchipis less expensive to set up.The two are equally expensive to evaluate.
References
[1] Fritsch, F. N. and R. E. Carlson. "Monotone Piecewise Cubic Interpolation." SIAM Journal on Numerical Analysis. Vol. 17, 1980, pp.238–246.
[2] Kahaner, David, Cleve Moler, Stephen Nash. Numerical Methods and Software. Upper Saddle River, NJ: Prentice Hall, 1988.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Input
xmust be strictly increasing.Code generation does not remove
yentries withNaNvalues.If you generate code for the
pp = pchip(x,y)syntax, then you cannot inputppto theppvalfunction in MATLAB®. To create a MATLABppstructure from appstructure created by the code generator:In code generation, use
unmkppto return the piecewise polynomial details to MATLAB.In MATLAB, use
mkppto create theppstructure.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
The
pchip(syntax is not supported for distributed arrays.x,y)
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)