qz
Generalized Schur (QZ) factorization for generalized eigenvalues
Description
Examples
QZ Factorization
Calculate the QZ factorization of two 3-by-3 matrices.
A = [1 7 3; 2 9 12; 5 22 7]; B = [3 1 0; 0 3 1; 0 0 3]; [AA,BB,Q,Z] = qz(A,B)
AA = 3×3
23.5574 1.4134 -14.3485
0 -0.5776 2.7629
0 0 -8.6720
BB = 3×3
3.5845 -0.1090 -0.6024
0 2.7599 0.8430
0 0 2.7292
Q = 3×3
0.2566 0.6353 0.7284
-0.9477 0.3134 0.0604
-0.1899 -0.7058 0.6824
Z = 3×3
0.1502 -0.9664 -0.2088
0.4689 0.2556 -0.8455
0.8704 0.0291 0.4915
Verify that the norms of AA - Q*A*Z, BB - Q*B*Z, Q'*Q - eye(size(Q)), and Z'*Z - eye(size(Z)) are 0, within machine precision.
norm(AA - Q*A*Z)
ans = 1.1982e-14
norm(BB - Q*B*Z)
ans = 2.6332e-15
norm(Q'*Q - eye(size(Q)))
ans = 4.4784e-16
norm(Z'*Z - eye(size(Z)))
ans = 7.2042e-16
Generalized Eigenvectors
Calculate the QZ factorization and also return the generalized eigenvectors of two 2-by-2 matrices.
A = [10 -7; -3 2]; B = [7 3; 12 9]; [AA,BB,Q,Z,V,W] = qz(A,B)
AA = 2×2
11.9600 -4.3532
0 -0.0836
BB = 2×2
1.6381 -2.9374
0 16.4830
Q = 2×2
-0.9597 0.2811
0.2811 0.9597
Z = 2×2
-0.5752 0.8180
0.8180 0.5752
V = 2×2
-0.7031 0.6960
1.0000 1.0000
W = 2×2
-1.0000 0.2929
0.4537 1.0000
Verify that the elements of Q*A*Z - AA and Q*B*Z - BB are 0, within machine precision.
Q*A*Z - AA
ans = 2×2
10-14 ×
0 0.1776
-0.1034 -0.1180
Q*B*Z - BB
ans = 2×2
10-14 ×
-0.0222 0
0.0888 -0.3553
Calculate the generalized eigenvalues and right and left eigenvectors of A and B by using the eig function. Verify that the elements of A*V - B*V*D and W'*A - D*W'*B are 0, within machine precision.
[V,D,W] = eig(A,B); A*V - B*V*D
ans = 2×2
10-14 ×
0 0.2054
0.7105 0.0333
W'*A - D*W'*B
ans = 2×2
10-14 ×
-0.7105 0.3553
0.0805 0.0319
Complex QZ Factorization
Calculate the complex QZ factorization of two 3-by-3 matrices.
A = [1/sqrt(2) 1 0; 0 1 1; 0 1/sqrt(2) 1]; B = [0 1 1; -1/sqrt(2) 0 1; 1 -1/sqrt(2) 0]; [AAc,BBc,Qc,Zc] = qz(A,B)
AAc = 3×3 complex
0.5011 - 0.8679i 0.0332 - 1.0852i 0.3687 + 0.9278i
0.0000 + 0.0000i 0.1848 - 0.0000i -0.6334 - 0.3673i
0.0000 + 0.0000i 0.0000 + 0.0000i 0.5590 + 0.9682i
BBc = 3×3 complex
1.0022 + 0.0000i 0.3136 + 0.0711i -0.0280 + 0.5966i
0.0000 + 0.0000i 1.3388 + 0.0000i 0.1572 + 0.6846i
0.0000 + 0.0000i 0.0000 + 0.0000i 1.1180 + 0.0000i
Qc = 3×3 complex
0.5379 + 0.2210i 0.4604 - 0.3553i 0.3214 - 0.4693i
0.2172 + 0.3386i 0.4018 - 0.0188i -0.7698 + 0.2895i
-0.3719 - 0.6014i 0.7068 - 0.0213i -0.0000 - 0.0000i
Zc = 3×3 complex
0.2514 + 0.0413i -0.7279 - 0.4531i -0.4470 - 0.0135i
-0.1000 - 0.6068i 0.3328 - 0.3332i -0.3326 + 0.5379i
0.6391 + 0.3853i 0.1423 - 0.1511i 0.2996 + 0.5570i
Calculate the real QZ decomposition of A and B by specifying mode as "real". The generalized Schur form of A is quasitriangular, indicating that it has complex eigenvalues.
[AAr,BBr,Qr,Zr] = qz(A,B,"real")AAr = 3×3
0.1464 -1.1759 -0.3094
0 1.0360 1.2594
0 -0.8587 0.3212
BBr = 3×3
1.0607 0.5952 -0.1441
0 1.6676 0
0 0 0.8481
Qr = 3×3
0.0000 -0.0000 -1.0000
0.7882 0.6154 -0.0000
0.6154 -0.7882 0.0000
Zr = 3×3
-0.7071 -0.2610 0.6572
0.5000 0.4727 0.7257
-0.5000 0.8417 -0.2037
For triangular AAc, compute the eigenvalues by using diag(AA)./diag(BB).
diag(AAc)./diag(BBc)
ans = 3×1 complex
0.5000 - 0.8660i
0.1381 - 0.0000i
0.5000 + 0.8660i
For quasitriangular AAr, compute the eigenvalues by using the ordeig function.
ordeig(AAr,BBr)
ans = 3×1 complex
0.1381 + 0.0000i
0.5000 + 0.8660i
0.5000 - 0.8660i
Input Arguments
A, B — Input matrices
square matrices
Input matrices, specified as real or complex square matrices. The dimensions of
A and B must be the same.
Data Types: single | double
Complex Number Support: Yes
mode — Decomposition mode
"complex" (default) | "real"
Decomposition mode, specified as one of these values:
"complex"—qzreturns a possibly complex decomposition, andAAandBBare triangular."real"—qzreturns a real decomposition, andAAandBBare quasitriangular.
Output Arguments
AA, BB — Generalized Schur forms of A and B
square matrices
Generalized Schur forms of A and B,
returned as upper triangular or quasitriangular square matrices.
When the decomposition is complex and
AAis triangular, then the diagonal elementsa = diag(AA)andb = diag(BB)are the generalized eigenvalues that satisfyA*V*b = B*V*aandb'*W'*A = a'*W'*B.When the decomposition is real and
AAis quasitriangular, you must further reduce the 2-by-2 blocks to obtain the eigenvalues of the full system. Each 2-by-2 block inAAcorresponds to a 2-by-2 diagonal block at the same location inBB.
Q, Z — Unitary factors
square matrices
Unitary factors, returned as square matrices that satisfy Q*A*Z =
AA and Q*B*Z = BB.
V — Right eigenvectors
square matrix
Right eigenvectors, returned as a square matrix whose columns are the generalized
right eigenvectors of the pair (A,B). The eigenvectors satisfy
A*V = B*V*D, where D contains the generalized
eigenvalues of the pair along its main diagonal. Use the eig function to return D and the ordeig function to return the diagonal elements of
D.
Different machines and releases of MATLAB® can produce different eigenvectors that are still numerically accurate:
For real eigenvectors, the sign of the eigenvectors can change.
For complex eigenvectors, the eigenvectors can be multiplied by any complex number of magnitude 1.
For a multiple eigenvalue, its eigenvectors can be recombined through linear combinations. For example, if Ax = λx and Ay = λy, then A(x+y) = λ(x+y), so x+y also is an eigenvector of A.
W — Left eigenvectors
square matrix
Left eigenvectors, returned as a square matrix whose columns are the generalized
left eigenvectors of the pair (A,B). The eigenvectors satisfy
W'*A = D*W'*B, where D contains the generalized
eigenvalues of the pair along its main diagonal. Use the eig
function to return D and the ordeig function to
return the diagonal elements of D.
Different machines and releases of MATLAB can produce different eigenvectors that are still numerically accurate:
For real eigenvectors, the sign of the eigenvectors can change.
For complex eigenvectors, the eigenvectors can be multiplied by any complex number of magnitude 1.
For a multiple eigenvalue, its eigenvectors can be recombined through linear combinations. For example, if Ax = λx and Ay = λy, then A(x+y) = λ(x+y), so x+y also is an eigenvector of A.
More About
Quasitriangular Matrix
An upper quasitriangular matrix can result from the Schur decomposition or generalized Schur (QZ) decomposition of a real matrix. An upper quasitriangular matrix is block upper triangular, with 1-by-1 and 2-by-2 blocks of nonzero values along the diagonal.
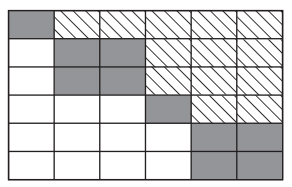
The eigenvalues of these diagonal blocks are also the eigenvalues of the matrix. The 1-by-1 blocks correspond to real eigenvalues, and the 2-by-2 blocks correspond to complex conjugate eigenvalue pairs.
Unitary Matrix
An invertible complex square matrix U is unitary if its conjugate
transpose is also its inverse, that is, if .
Tips
You can calculate the generalized eigenvalues that solve the generalized eigenvalue problem from the QZ factorization. For triangular
AA, calculate the eigenvalues usingdiag(AA)./diag(BB). For quasitriangularAA, calculate the eigenvalues usingordeig(AA,BB).
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)