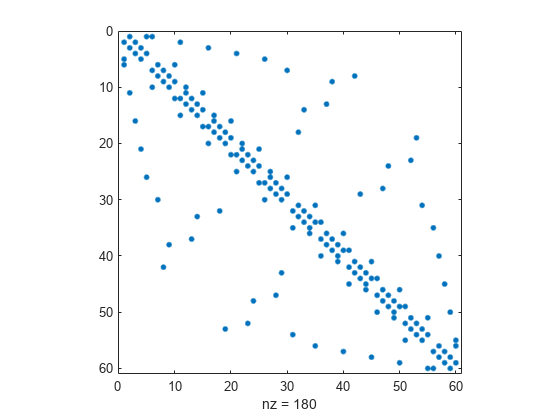
sprandn
Sparse normally distributed random matrix
Description
R = sprandn(S)S, but
with normally distributed random entries with mean 0 and variance
1.
Examples
Input Arguments
Limitations
sprandnis designed to produce large matrices with small density and will generate significantly fewer nonzero values than requested ifm*nis small ordensityis large.