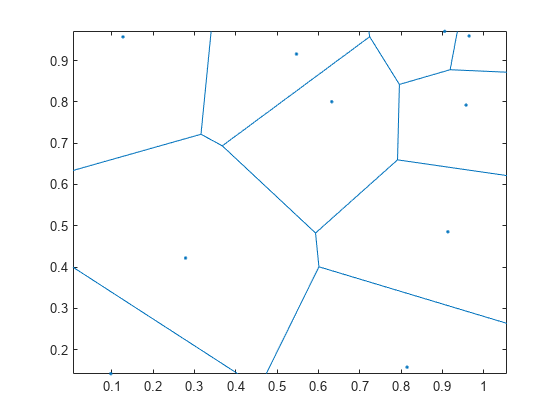
voronoi
Voronoi diagram
Description
voronoi(
plots the bounded cells of the Voronoi diagram for the 2-D points in vectors x,y)x and
y.
voronoi( uses the TO)delaunayTriangulation object
TO to plot the Voronoi diagram.
h = voronoi(___)
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced before R2006a