fminimax
Solve minimax constraint problem
Syntax
Description
fminimax seeks a point that minimizes the maximum of a set of
objective functions.
The problem includes any type of constraint. In detail, fminimax
seeks the minimum of a problem specified by
where b and beq are vectors, A and Aeq are matrices, and c(x), ceq(x), and F(x) are functions that return vectors. F(x), c(x), and ceq(x) can be nonlinear functions.
x, lb, and ub can be passed as vectors or matrices; see Matrix Arguments.
You can also solve max-min problems with fminimax, using the
identity
You can solve problems of the form
by using the AbsoluteMaxObjectiveCount option; see Solve Minimax Problem Using Absolute Value of One Objective.
x = fminimax(fun,x0)x0 and finds a minimax solution x to the
functions described in fun.
Note
Passing Extra Parameters explains how to pass extra parameters to the objective functions and nonlinear constraint functions, if necessary.
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)lb ≤ x ≤ ub.
If no equalities exist, set Aeq = [] and beq = []. If
x(i) is unbounded below, set lb(i) = –Inf; if
x(i) is unbounded above, set ub(i) = Inf.
Note
Note
If the specified input bounds for a problem are inconsistent, the output
x is x0 and the output fval
is [].
Examples
Minimize Maximum of sin and cos
Create a plot of the sin and cos functions and their maximum over the interval [–pi,pi].
t = linspace(-pi,pi); plot(t,sin(t),'r-') hold on plot(t,cos(t),'b-'); plot(t,max(sin(t),cos(t)),'ko') legend('sin(t)','cos(t)','max(sin(t),cos(t))','Location','NorthWest')
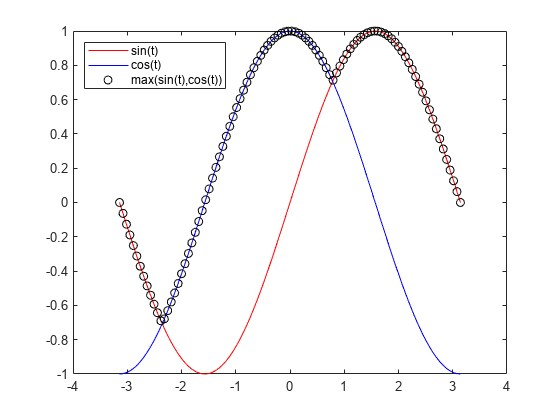
The plot shows two local minima of the maximum, one near 1, and the other near –2. Find the minimum near 1.
fun = @(x)[sin(x);cos(x)]; x0 = 1; x1 = fminimax(fun,x0)
Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x1 = 0.7854
Find the minimum near –2.
x0 = -2; x2 = fminimax(fun,x0)
Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x2 = -2.3562
Solve Linearly Constrained Minimax Problem
The objective functions for this example are linear plus constants. For a description and plot of the objective functions, see Compare fminimax and fminunc.
Set the objective functions as three linear functions of the form for three vectors and three constants .
a = [1;1]; b = [-1;1]; c = [0;-1]; a0 = 2; b0 = -3; c0 = 4; fun = @(x)[x*a+a0,x*b+b0,x*c+c0];
Find the minimax point subject to the inequality x(1) + 3*x(2) <= –4.
A = [1,3]; b = -4; x0 = [-1,-2]; x = fminimax(fun,x0,A,b)
Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x = 1×2
-5.8000 0.6000
Solve Bound-Constrained Minimax Problem
The objective functions for this example are linear plus constants. For a description and plot of the objective functions, see Compare fminimax and fminunc.
Set the objective functions as three linear functions of the form for three vectors and three constants .
a = [1;1]; b = [-1;1]; c = [0;-1]; a0 = 2; b0 = -3; c0 = 4; fun = @(x)[x*a+a0,x*b+b0,x*c+c0];
Set bounds that –2 <= x(1) <= 2 and –1 <= x(2) <= 1 and solve the minimax problem starting from [0,0].
lb = [-2,-1];
ub = [2,1];
x0 = [0,0];
A = []; % No linear constraints
b = [];
Aeq = [];
beq = [];
[x,fval] = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x = 1×2
-0.0000 1.0000
fval = 1×3
3.0000 -2.0000 3.0000
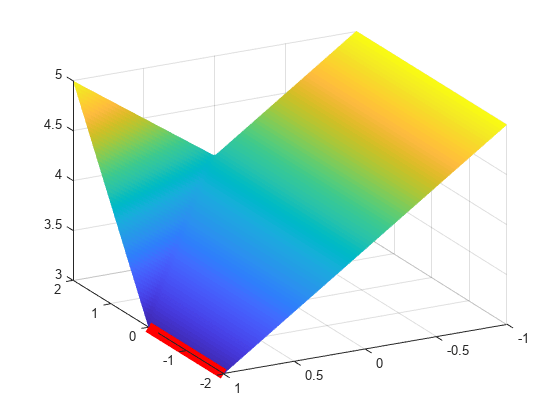
In this case, the solution is not unique. Many points satisfy the constraints and have the same minimax value. Plot the surface representing the maximum of the three objective functions, and plot a red line showing the points that have the same minimax value.
[X,Y] = meshgrid(linspace(-2,2),linspace(-1,1)); Z = max(fun([X(:),Y(:)]),[],2); Z = reshape(Z,size(X)); surf(X,Y,Z,'LineStyle','none') view(-118,28) hold on line([-2,0],[1,1],[3,3],'Color','r','LineWidth',8) hold off
Find Minimax Subject to Nonlinear Constraints
The objective functions for this example are linear plus constants. For a description and plot of the objective functions, see Compare fminimax and fminunc.
Set the objective functions as three linear functions of the form for three vectors and three constants .
a = [1;1]; b = [-1;1]; c = [0;-1]; a0 = 2; b0 = -3; c0 = 4; fun = @(x)[x*a+a0,x*b+b0,x*c+c0];
The unitdisk function represents the nonlinear inequality constraint .
type unitdiskfunction [c,ceq] = unitdisk(x) c = x(1)^2 + x(2)^2 - 1; ceq = [];
Solve the minimax problem subject to the unitdisk constraint, starting from x0 = [0,0].
x0 = [0,0];
A = []; % No other constraints
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = @unitdisk;
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x = 1×2
-0.0000 1.0000
Solve Minimax Problem Using Absolute Value of One Objective
fminimax can minimize the maximum of either or for the first several values of by using the AbsoluteMaxObjectiveCount option. To minimize the absolute values of of the objectives, arrange the objective function values so that through are the objectives for absolute minimization, and set the AbsoluteMaxObjectiveCount option to k.
In this example, minimize the maximum of sin and cos, specify sin as the first objective, and set AbsoluteMaxObjectiveCount to 1.
fun = @(x)[sin(x),cos(x)]; options = optimoptions('fminimax','AbsoluteMaxObjectiveCount',1); x0 = 1; A = []; % No constraints b = []; Aeq = []; beq = []; lb = []; ub = []; nonlcon = []; x1 = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x1 = 0.7854
Try starting from x0 = –2.
x0 = -2; x2 = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x2 = -3.1416
Plot the function.
t = linspace(-pi,pi); plot(t,max(abs(sin(t)),cos(t)))
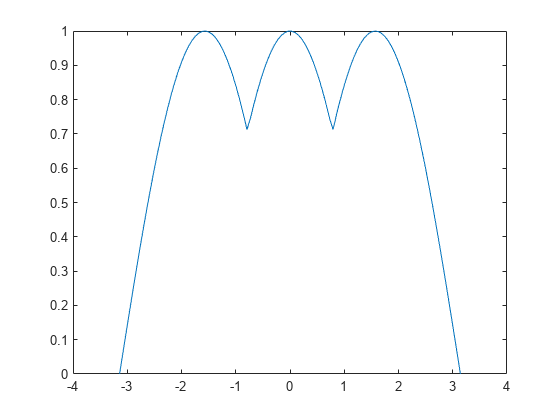
To see the effect of the AbsoluteMaxObjectiveCount option, compare this plot to the plot in the example Minimize Maximum of sin and cos.
Obtain Minimax Value
Obtain both the location of the minimax point and the value of the objective functions. For a description and plot of the objective functions, see Compare fminimax and fminunc.
Set the objective functions as three linear functions of the form for three vectors and three constants .
a = [1;1]; b = [-1;1]; c = [0;-1]; a0 = 2; b0 = -3; c0 = 4; fun = @(x)[x*a+a0,x*b+b0,x*c+c0];
Set the initial point to [0,0] and find the minimax point and value.
x0 = [0,0]; [x,fval] = fminimax(fun,x0)
Local minimum possible. Constraints satisfied. fminimax stopped because the size of the current search direction is less than twice the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
x = 1×2
-2.5000 2.2500
fval = 1×3
1.7500 1.7500 1.7500
All three objective functions have the same value at the minimax point. Unconstrained problems typically have at least two objectives that are equal at the solution, because if a point is not a local minimum for any objective and only one objective has the maximum value, then the maximum objective can be lowered.
Obtain All Minimax Outputs
The objective functions for this example are linear plus constants. For a description and plot of the objective functions, see Compare fminimax and fminunc.
Set the objective functions as three linear functions of the form for three vectors and three constants .
a = [1;1]; b = [-1;1]; c = [0;-1]; a0 = 2; b0 = -3; c0 = 4; fun = @(x)[x*a+a0,x*b+b0,x*c+c0];
Find the minimax point subject to the inequality x(1) + 3*x(2) <= –4.
A = [1,3]; b = -4; x0 = [-1,-2];
Set options for iterative display, and obtain all solver outputs.
options = optimoptions('fminimax','Display','iter'); Aeq = []; % No other constraints beq = []; lb = []; ub = []; nonlcon = []; [x,fval,maxfval,exitflag,output,lambda] =... fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Objective Max Line search Directional
Iter F-count value constraint steplength derivative Procedure
0 4 0 6
1 9 5 0 1 0.981
2 14 4.889 0 1 -0.302 Hessian modified twice
3 19 3.4 8.132e-09 1 -0.302 Hessian modified twice
Local minimum possible. Constraints satisfied.
fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are
satisfied to within the value of the constraint tolerance.
x = 1×2
-5.8000 0.6000
fval = 1×3
-3.2000 3.4000 3.4000
maxfval = 3.4000
exitflag = 4
output = struct with fields:
iterations: 4
funcCount: 19
lssteplength: 1
stepsize: 6.0684e-10
algorithm: 'active-set'
firstorderopt: []
constrviolation: 8.1323e-09
message: 'Local minimum possible. Constraints satisfied....'
lambda = struct with fields:
lower: [2x1 double]
upper: [2x1 double]
eqlin: [0x1 double]
eqnonlin: [0x1 double]
ineqlin: 0.2000
ineqnonlin: [0x1 double]
Examine the returned information:
Two objective function values are equal at the solution.
The solver converges in 4 iterations and 19 function evaluations.
The
lambda.ineqlinvalue is nonzero, indicating that the linear constraint is active at the solution.
Input Arguments
fun — Objective functions
function handle | function name
Objective functions, specified as a function handle or function name.
fun is a function that accepts a vector x and
returns a vector F, the objective functions evaluated at
x. You can specify the function fun as a
function handle for a function file:
x = fminimax(@myfun,x0,goal,weight)
where myfun is a MATLAB® function such as
function F = myfun(x) F = ... % Compute function values at x.
fun can also be a function handle for an anonymous
function:
x = fminimax(@(x)sin(x.*x),x0,goal,weight);
fminimax passes x to
your objective function and any nonlinear constraint functions in the shape of the
x0 argument. For example, if x0 is a 5-by-3 array,
then fminimax passes x to fun as a
5-by-3 array. However, fminimax multiplies linear constraint matrices
A or Aeq with x after
converting x to the column vector x(:).
To minimize the worst-case absolute values of some elements of the vector
F(x) (that is, min{max
abs{F(x)} } ), partition those objectives into
the first elements of F and use optimoptions to set the
AbsoluteMaxObjectiveCount option to the number of these objectives. These
objectives must be partitioned into the first elements of the
vector F returned by fun. For an example, see
Solve Minimax Problem Using Absolute Value of One Objective.
Assume that the gradients of the objective functions can also be computed
and the SpecifyObjectiveGradient option is
true, as set by:
options = optimoptions('fminimax','SpecifyObjectiveGradient',true)
In this case, the function fun must return, in the second output
argument, the gradient values G (a matrix) at x.
The gradient consists of the partial derivative dF/dx of each
F at the point x. If F is a
vector of length m and x has length
n, where n is the length of
x0, then the gradient G of
F(x) is an n-by-m matrix
where G(i,j) is the partial derivative of F(j)
with respect to x(i) (that is, the jth column of
G is the gradient of the jth objective function
F(j)). If you define F as an array, then the
preceding discussion applies to F(:), the linear ordering of the
F array. In any case, G is a 2-D matrix.
Note
Setting SpecifyObjectiveGradient to true is
effective only when the problem has no nonlinear constraint, or when the problem has a
nonlinear constraint with SpecifyConstraintGradient set to
true. Internally, the objective is folded into the constraints,
so the solver needs both gradients (objective and constraint) supplied in order to
avoid estimating a gradient.
Data Types: char | string | function_handle
x0 — Initial point
real vector | real array
Initial point, specified as a real vector or real array. Solvers use the number of elements in
x0 and the size of x0 to determine the number
and size of variables that fun accepts.
Example: x0 = [1,2,3,4]
Data Types: double
A — Linear inequality constraints
real matrix
Linear inequality constraints, specified as a real matrix. A is
an M-by-N matrix, where M is
the number of inequalities, and N is the number
of variables (number of elements in x0). For
large problems, pass A as a sparse matrix.
A encodes the M linear
inequalities
A*x <= b,
where x is the column vector of N variables x(:),
and b is a column vector with M elements.
For example, consider these inequalities:
x1 + 2x2 ≤
10
3x1 +
4x2 ≤ 20
5x1 +
6x2 ≤ 30,
Specify the inequalities by entering the following constraints.
A = [1,2;3,4;5,6]; b = [10;20;30];
Example: To specify that the x components sum to 1 or less, use A =
ones(1,N) and b = 1.
Data Types: double
b — Linear inequality constraints
real vector
Linear inequality constraints, specified as a real vector. b is
an M-element vector related to the A matrix.
If you pass b as a row vector, solvers internally
convert b to the column vector b(:).
For large problems, pass b as a sparse vector.
b encodes the M linear
inequalities
A*x <= b,
where x is the column vector of N variables x(:),
and A is a matrix of size M-by-N.
For example, consider these inequalities:
x1
+ 2x2 ≤
10
3x1
+ 4x2 ≤
20
5x1
+ 6x2 ≤
30.
Specify the inequalities by entering the following constraints.
A = [1,2;3,4;5,6]; b = [10;20;30];
Example: To specify that the x components sum to 1 or less, use A =
ones(1,N) and b = 1.
Data Types: double
Aeq — Linear equality constraints
real matrix
Linear equality constraints, specified as a real matrix. Aeq is
an Me-by-N matrix, where Me is
the number of equalities, and N is the number of
variables (number of elements in x0). For large
problems, pass Aeq as a sparse matrix.
Aeq encodes the Me linear
equalities
Aeq*x = beq,
where x is the column vector of N variables x(:),
and beq is a column vector with Me elements.
For example, consider these inequalities:
x1 + 2x2 +
3x3 = 10
2x1 +
4x2 + x3 =
20,
Specify the inequalities by entering the following constraints.
Aeq = [1,2,3;2,4,1]; beq = [10;20];
Example: To specify that the x components sum to 1, use Aeq = ones(1,N) and
beq = 1.
Data Types: double
beq — Linear equality constraints
real vector
Linear equality constraints, specified as a real vector. beq is
an Me-element vector related to the Aeq matrix.
If you pass beq as a row vector, solvers internally
convert beq to the column vector beq(:).
For large problems, pass beq as a sparse vector.
beq encodes the Me linear
equalities
Aeq*x = beq,
where x is the column vector of N variables
x(:), and Aeq is a matrix of size
Me-by-N.
For example, consider these equalities:
x1
+ 2x2 +
3x3 =
10
2x1
+ 4x2 +
x3 =
20.
Specify the equalities by entering the following constraints.
Aeq = [1,2,3;2,4,1]; beq = [10;20];
Example: To specify that the x components sum to 1, use Aeq = ones(1,N) and
beq = 1.
Data Types: double
lb — Lower bounds
real vector | real array
Lower bounds, specified as a real vector or real array. If the number of elements in
x0 is equal to the number of elements in lb,
then lb specifies that
x(i) >= lb(i) for all i.
If numel(lb) < numel(x0), then lb specifies
that
x(i) >= lb(i) for 1 <=
i <= numel(lb).
If lb has fewer elements than x0, solvers issue a
warning.
Example: To specify that all x components are positive, use lb =
zeros(size(x0)).
Data Types: double
ub — Upper bounds
real vector | real array
Upper bounds, specified as a real vector or real array. If the number of elements in
x0 is equal to the number of elements in ub,
then ub specifies that
x(i) <= ub(i) for all i.
If numel(ub) < numel(x0), then ub specifies
that
x(i) <= ub(i) for 1 <=
i <= numel(ub).
If ub has fewer elements than x0, solvers issue
a warning.
Example: To specify that all x components are less than 1, use ub =
ones(size(x0)).
Data Types: double
nonlcon — Nonlinear constraints
function handle | function name
Nonlinear constraints, specified as a function handle or function name. nonlcon is a function that accepts a vector or array x and returns two arrays, c(x) and ceq(x).
c(x)is the array of nonlinear inequality constraints atx.fminimaxattempts to satisfyc(x) <= 0for all entries ofc.ceq(x)is the array of nonlinear equality constraints atx.fminimaxattempts to satisfyceq(x) = 0for all entries ofceq.
For example,
x = fminimax(@myfun,x0,...,@mycon)
where mycon is a MATLAB function such as the
following:
function [c,ceq] = mycon(x) c = ... % Compute nonlinear inequalities at x. ceq = ... % Compute nonlinear equalities at x.
Suppose that the gradients of the constraints can also be computed and
the SpecifyConstraintGradient option is true, as
set by:
options = optimoptions('fminimax','SpecifyConstraintGradient',true)In this case, the function nonlcon must also return, in the third and
fourth output arguments, GC, the gradient of c(x),
and GCeq, the gradient of ceq(x). See Nonlinear Constraints for an explanation of how to “conditionalize” the
gradients for use in solvers that do not accept supplied gradients.
If nonlcon returns a vector c of m
components and x has length n, where
n is the length of x0, then the gradient
GC of c(x) is an
n-by-m matrix, where
GC(i,j) is the partial derivative of c(j) with
respect to x(i) (that is, the jth column of
GC is the gradient of the jth inequality
constraint c(j)). Likewise, if ceq has
p components, the gradient GCeq of
ceq(x) is an n-by-p matrix,
where GCeq(i,j) is the partial derivative of
ceq(j) with respect to x(i) (that is, the
jth column of GCeq is the gradient of the
jth equality constraint ceq(j)).
Note
Setting SpecifyConstraintGradient to true is
effective only when SpecifyObjectiveGradient is set to
true. Internally, the objective is folded into the
constraint, so the solver needs both gradients (objective and constraint) supplied
in order to avoid estimating a gradient.
Note
Because Optimization Toolbox™ functions accept only inputs of type double,
user-supplied objective and nonlinear constraint functions must return outputs of
type double.
See Passing Extra Parameters for an explanation of how to parameterize the
nonlinear constraint function nonlcon, if necessary.
Data Types: char | function_handle | string
options — Optimization options
output of optimoptions | structure such as optimset returns
Optimization options, specified as the output of optimoptions
or a structure such as optimset returns.
Some options are absent from the
optimoptions display. These options appear in italics in the following
table. For details, see View Optimization Options.
For details about options that have different names for
optimset, see Current and Legacy Option Names.
| Option | Description |
|---|---|
AbsoluteMaxObjectiveCount | Number of elements of Fi(x) for which to minimize the absolute value of Fi. See Solve Minimax Problem Using Absolute Value of One Objective. For |
ConstraintTolerance | Termination tolerance on the constraint violation (a nonnegative
scalar). The default is For
|
| Diagnostics | Display of diagnostic information about the function to be minimized
or solved. The choices are |
| DiffMaxChange | Maximum change in variables for finite-difference gradients (a
positive scalar). The default is |
| DiffMinChange | Minimum change in variables for finite-difference gradients (a
positive scalar). The default is |
| Level of display (see Iterative Display):
|
FiniteDifferenceStepSize |
Scalar or vector step size factor for finite differences. When
you set
sign′(x) = sign(x) except sign′(0) = 1.
Central finite differences are
FiniteDifferenceStepSize expands to a vector. The default
is sqrt(eps) for forward finite differences, and eps^(1/3)
for central finite differences.
For |
FiniteDifferenceType | Type of finite differences used to estimate gradients, either
The algorithm is careful to obey bounds when estimating both types of finite differences. For example, it might take a backward difference, rather than a forward difference, to avoid evaluating at a point outside the bounds. For
|
FunctionTolerance | Termination tolerance on the function value (a nonnegative scalar).
The default is For
|
| FunValCheck | Check that signifies whether the objective function and constraint
values are valid. |
MaxFunctionEvaluations | Maximum number of function evaluations allowed (a nonnegative
integer). The default is For
|
MaxIterations | Maximum number of iterations allowed (a nonnegative integer). The
default is For
|
| MaxSQPIter | Maximum number of SQP iterations allowed (a positive integer). The
default is |
| MeritFunction | If this option is set to |
OptimalityTolerance | Termination tolerance on the first-order optimality (a
nonnegative scalar). The default is For |
OutputFcn | One or more user-defined functions that an optimization function
calls at each iteration. Pass a function handle or a cell array of function
handles. The default is none ( |
PlotFcn | Plots showing various measures of progress while the algorithm
executes. Select from predefined plots or write your own. Pass a name,
function handle, or cell array of names or function handles. For custom plot
functions, pass function handles. The default is none
(
Custom plot functions use the same syntax as output functions. See Output Functions for Optimization Toolbox and Output Function and Plot Function Syntax. For |
| RelLineSrchBnd | Relative bound (a real nonnegative scalar value) on the line search
step length such that the total displacement in |
| RelLineSrchBndDuration | Number of iterations for which the bound specified in
|
SpecifyConstraintGradient | Gradient for nonlinear constraint functions defined by the user. When
this option is set to For
|
SpecifyObjectiveGradient | Gradient for the objective function defined by the user. Refer to the
description of For |
StepTolerance | Termination tolerance on For
|
| TolConSQP | Termination tolerance on the inner iteration SQP constraint violation
(a positive scalar). The default is |
TypicalX | Typical |
UseParallel | Option for using parallel computing. When this option is set to
|
Example: optimoptions('fminimax','PlotFcn','optimplotfval')
problem — Problem structure
structure
Problem structure, specified as a structure with the fields in this table.
| Field Name | Entry |
|---|---|
| Objective function fun |
| Initial point for x |
| Matrix for linear inequality constraints |
| Vector for linear inequality constraints |
| Matrix for linear equality constraints |
| Vector for linear equality constraints |
lb | Vector of lower bounds |
ub | Vector of upper bounds |
| Nonlinear constraint function |
| 'fminimax' |
| Options created with optimoptions |
You must supply at least the objective, x0,
solver, and options fields in the
problem structure.
Data Types: struct
Output Arguments
x — Solution
real vector | real array
Solution, returned as a real vector or real array. The size
of x is the same as the size of x0.
Typically, x is a local solution to the problem
when exitflag is positive. For information on
the quality of the solution, see When the Solver Succeeds.
fval — Objective function values at solution
real array
Objective function values at the solution, returned as a real array. Generally,
fval = fun(x).
maxfval — Maximum of objective function values at solution
real scalar
Maximum of the objective function values at the solution, returned as a real scalar.
maxfval = max(fval(:)).
exitflag — Reason fminimax stopped
integer
Reason fminimax stopped, returned as an integer.
| Function converged to a solution
|
| Magnitude of the search direction was less than the specified
tolerance, and the constraint violation was less than
|
| Magnitude of the directional derivative was less than the
specified tolerance, and the constraint violation was less than
|
| Number of iterations exceeded
|
| Stopped by an output function or plot function |
| No feasible point was found. |
output — Information about optimization process
structure
Information about the optimization process, returned as a structure with the fields in this table.
iterations | Number of iterations taken |
funcCount | Number of function evaluations |
lssteplength | Size of the line search step relative to the search direction |
constrviolation | Maximum of the constraint functions |
stepsize | Length of the last displacement in
|
algorithm | Optimization algorithm used |
firstorderopt | Measure of first-order optimality |
message | Exit message |
lambda — Lagrange multipliers at solution
structure
Lagrange multipliers at the solution, returned as a structure with the fields in this table.
Algorithms
fminimax solves a minimax problem by converting it into a goal
attainment problem, and then solving the converted goal attainment problem using
fgoalattain. The conversion sets all goals to 0 and all weights to 1.
See Equation 1 in
Multiobjective Optimization Algorithms.
Alternative Functionality
App
The Optimize Live Editor task provides a visual interface for fminimax.
Extended Capabilities
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To run in parallel, set the 'UseParallel' option to true.
options = optimoptions('solvername','UseParallel',true)
For more information, see Using Parallel Computing in Optimization Toolbox.
Version History
Introduced before R2006a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)