Two-Dimensional Semi-Infinite Constraint
Find values of x that minimize
f(x) = (x1 – 0.2)2 + (x2– 0.2)2 + (x3– 0.2)2,
where
for all values of w1 and w2 over the ranges
1 ≤ w1 ≤
100,
1 ≤ w2 ≤
100,
starting at the point x = [0.25,0.25,0.25].
Note that the semi-infinite constraint is two-dimensional, that is, a matrix.
First, write a file that computes the objective function.
function f = myfun(x,s) % Objective function f = sum((x-0.2).^2);
Second, write a file for the constraints, called mycon.m.
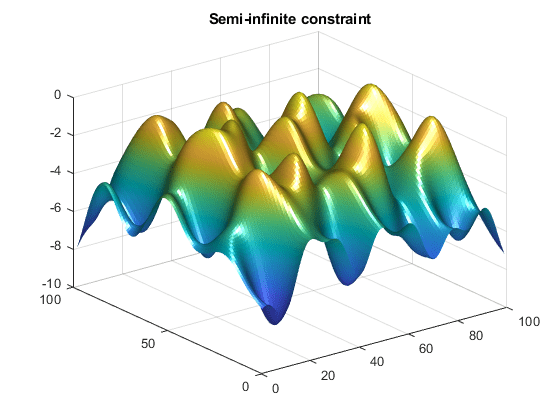
Include code to draw the surface plot of the semi-infinite constraint
each time mycon is called. This enables you to
see how the constraint changes as X is being minimized.
function [c,ceq,K1,s] = mycon(X,s) % Initial sampling interval if isnan(s(1,1)), s = [2 2]; end % Sampling set w1x = 1:s(1,1):100; w1y = 1:s(1,2):100; [wx,wy] = meshgrid(w1x,w1y); % Semi-infinite constraint K1 = sin(wx*X(1)).*cos(wx*X(2))-1/1000*(wx-50).^2 -... sin(wx*X(3))-X(3)+sin(wy*X(2)).*cos(wx*X(1))-... 1/1000*(wy-50).^2-sin(wy*X(3))-X(3)-1.5; % No finite nonlinear constraints c = []; ceq=[]; % Mesh plot m = surf(wx,wy,K1,'edgecolor','none','facecolor','interp'); camlight headlight title('Semi-infinite constraint') drawnow
Next, invoke an optimization routine.
x0 = [0.25, 0.25, 0.25]; % Starting guess
[x,fval] = fseminf(@myfun,x0,1,@mycon)After nine iterations, the solution is
x
x =
0.2523 0.1715 0.1938and the function value at the solution is
fval
fval =
0.0036The goal was to minimize the objective f(x)
such that the semi-infinite constraint satisfied K1(x,w) ≤ 1.5. Evaluating mycon at
the solution x and looking at the maximum element
of the matrix K1 shows the constraint is easily
satisfied.
[c,ceq,K1] = mycon(x,[0.5,0.5]); % Sampling interval 0.5
max(max(K1))ans = -0.0370
This call to mycon produces the following
surf plot, which shows the semi-infinite constraint at x.