Clamped Square Isotropic Plate with Uniform Pressure Load
This example shows how to calculate the deflection of a structural plate under a pressure loading.
The partial differential equation for a thin isotropic plate with a pressure loading is
where is the bending stiffness of the plate given by
and is the modulus of elasticity, is Poisson's ratio, is the plate thickness, is the transverse deflection of the plate, and is the pressure load.
The boundary conditions for the clamped boundaries are and , where is the derivative of in a direction normal to the boundary.
Partial Differential Equation Toolbox™ cannot directly solve this fourth-order plate equation. Convert the fourth-order equation to these two second-order partial differential equations, where is the new dependent variable.
You cannot directly specify boundary conditions for both and in this second-order system. Instead, specify that is 0, and define so that also equals 0 on the boundary. To specify these conditions, use stiff "springs" distributed along the boundary. The springs apply a transverse shear force to the plate edge. Define the shear force along the boundary due to these springs as , where is the normal to the boundary, and is the stiffness of the springs. This expression is a generalized Neumann boundary condition supported by the toolbox. The value of must be large enough so that is approximately 0 at all points on the boundary. It also must be small enough to avoid numerical errors due to an ill-conditioned stiffness matrix.
The toolbox uses the dependent variables and instead of and . Rewrite the two second-order partial differential equations using variables and :
Create a PDE model for a system of two equations.
model = createpde(2);
Create a square geometry and include it in the model.
len = 10; gdm = [3 4 0 len len 0 0 0 len len]'; g = decsg(gdm,'S1',('S1')'); geometryFromEdges(model,g);
Plot the geometry with the edge labels.
figure pdegplot(model,"EdgeLabels","on") ylim([-1,11]) axis equal title("Geometry With Edge Labels Displayed")
PDE coefficients must be specified using the format required by the toolbox. For details, see
The c coefficient in this example is a tensor, which can be represented as a 2-by-2 matrix of 2-by-2 blocks:
This matrix is further flattened into a column vector of six elements. The entries in the full 2-by-2 matrix (defining the coefficient a) and the 2-by-1 vector (defining the coefficient f) follow directly from the definition of the two-equation system.
E = 1.0e6; % Modulus of elasticity nu = 0.3; % Poisson's ratio thick = 0.1; % Plate thickness pres = 2; % External pressure D = E*thick^3/(12*(1 - nu^2)); c = [1 0 1 D 0 D]'; a = [0 0 1 0]'; f = [0 pres]'; specifyCoefficients(model,"m",0,"d",0,"c",c,"a",a,"f",f);
To define boundary conditions, first specify spring stiffness.
k = 1e7;
Define distributed springs on all four edges.
bOuter = applyBoundaryCondition(model,"neumann","Edge",(1:4),... "g",[0 0],"q",[0 0; k 0]);
Generate a mesh.
generateMesh(model);
Solve the model.
res = solvepde(model);
Access the solution at the nodal locations.
u = res.NodalSolution;
Plot the transverse deflection.
numNodes = size(model.Mesh.Nodes,2); figure pdeplot(model,"XYData",u(:,1),"Contour","on") title("Transverse Deflection")
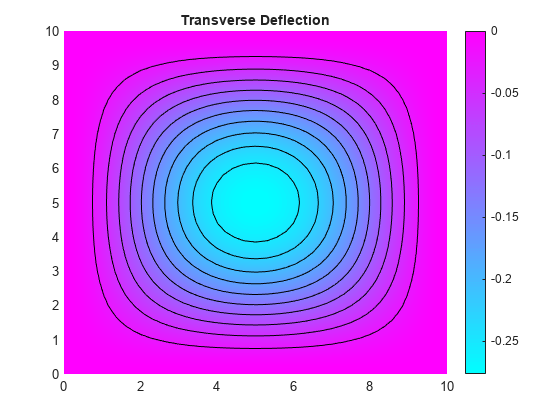
Find the transverse deflection at the plate center.
numNodes = size(model.Mesh.Nodes,2); wMax = min(u(1:numNodes,1))
wMax = -0.2762
Compare the result with the deflection at the plate center computed analytically.
wMax = -.0138*pres*len^4/(E*thick^3)
wMax = -0.2760
