Poisson's Equation on Unit Disk
This example shows how to numerically solve a Poisson's equation, compare the numerical solution with the exact solution, and refine the mesh until the solutions are close.
The Poisson equation on a unit disk with zero Dirichlet boundary condition can be written as in , on , where is the unit disk. The exact solution is
For most PDEs, the exact solution is not known. However, the Poisson's equation on a unit disk has a known, exact solution that you can use to see how the error decreases as you refine the mesh.
Problem Definition
Create the PDE model and include the geometry.
model = createpde(); geometryFromEdges(model,@circleg);
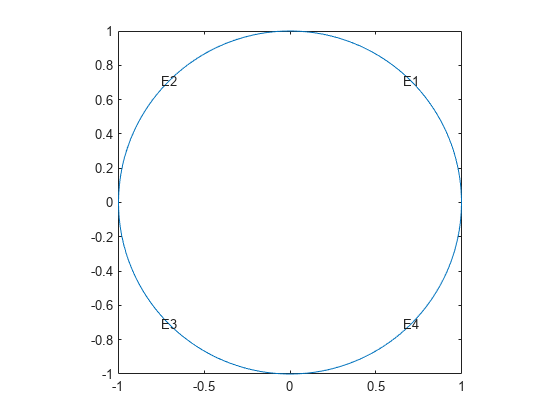
Plot the geometry and display the edge labels for use in the boundary condition definition.
figure pdegplot(model,"EdgeLabels","on"); axis equal
Specify zero Dirichlet boundary conditions on all edges.
applyBoundaryCondition(model,"dirichlet", ... "Edge",1:model.Geometry.NumEdges, ... "u",0);
Specify the coefficients.
specifyCoefficients(model,"m",0,"d",0,"c",1,"a",0,"f",1);
Solution and Error with a Coarse Mesh
Create a mesh with target maximum element size 0.1.
hmax = 0.1; generateMesh(model,"Hmax",hmax); figure pdemesh(model); axis equal

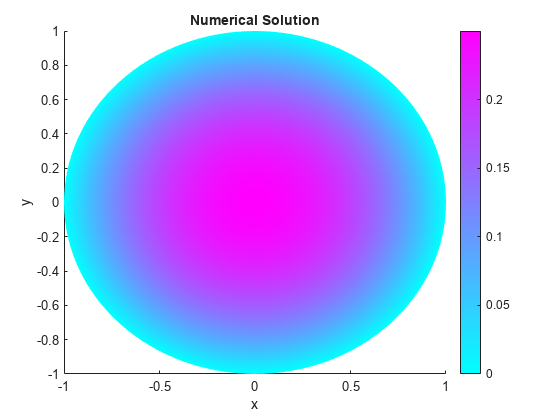
Solve the PDE and plot the solution.
results = solvepde(model); u = results.NodalSolution; pdeplot(model,"XYData",u) title("Numerical Solution"); xlabel("x") ylabel("y")
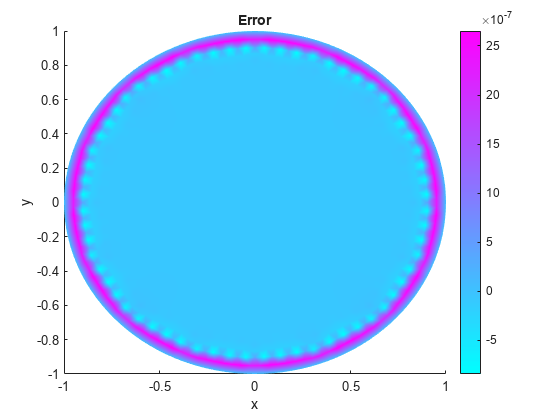
Compare this result with the exact analytical solution and plot the error.
p = model.Mesh.Nodes; exact = (1 - p(1,:).^2 - p(2,:).^2)/4; pdeplot(model,"XYData",u - exact') title("Error"); xlabel("x") ylabel("y")
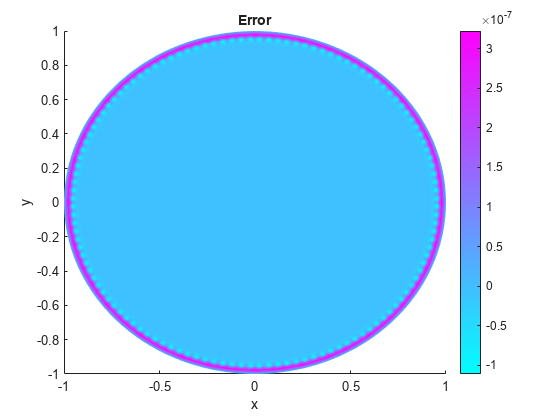
Solutions and Errors with Refined Meshes
Solve the equation while refining the mesh in each iteration and comparing the result with the exact solution. Each refinement halves the Hmax value. Refine the mesh until the infinity norm of the error vector is less than .
hmax = 0.1; error = []; err = 1; while err > 5e-7 % run until error <= 5e-7 generateMesh(model,"Hmax",hmax); % refine mesh results = solvepde(model); u = results.NodalSolution; p = model.Mesh.Nodes; exact = (1 - p(1,:).^2 - p(2,:).^2)/4; err = norm(u - exact',inf); % compare with exact solution error = [error err]; % keep history of err hmax = hmax/2; end
Plot the infinity norm of the error vector for each iteration. The value of the error decreases in each iteration.
plot(error,"rx","MarkerSize",12); ax = gca; ax.XTick = 1:numel(error); title("Error History"); xlabel("Iteration"); ylabel("Norm of Error");

Plot the final mesh and its corresponding solution.
figure
pdemesh(model);
axis equal
figure pdeplot(model,"XYData",u) title("Numerical Solution"); xlabel("x") ylabel("y")
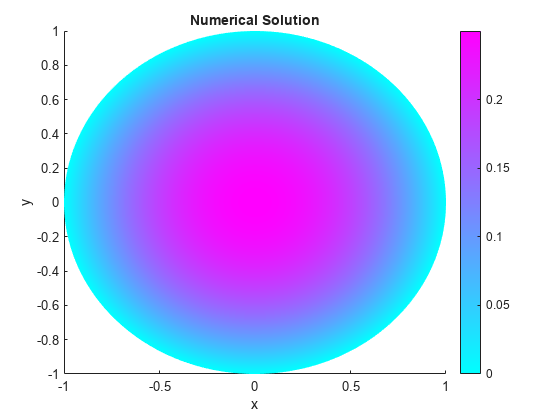
Compare the result with the exact analytical solution and plot the error.
p = model.Mesh.Nodes; exact = (1 - p(1,:).^2 - p(2,:).^2)/4; pdeplot(model,"XYData",u - exact') title("Error"); xlabel("x") ylabel("y")