plotGratingLobeDiagram
System object: phased.URA
Namespace: phased
Plot grating lobe diagram of array
Syntax
plotGratingLobeDiagram(H,FREQ)
plotGratingLobeDiagram(H,FREQ,ANGLE)
plotGratingLobeDiagram(H,FREQ,ANGLE,C)
plotGratingLobeDiagram(H,FREQ,ANGLE,C,F0)
hPlot = plotGratingLobeDiagram(___)
Description
plotGratingLobeDiagram( plots
the grating lobe diagram of an array in the u-v coordinate
system. The System object™ H,FREQ)H specifies the
array. The argument FREQ specifies the signal
frequency and phase-shifter frequency. The array, by default, is
steered to 0° azimuth and 0° elevation.
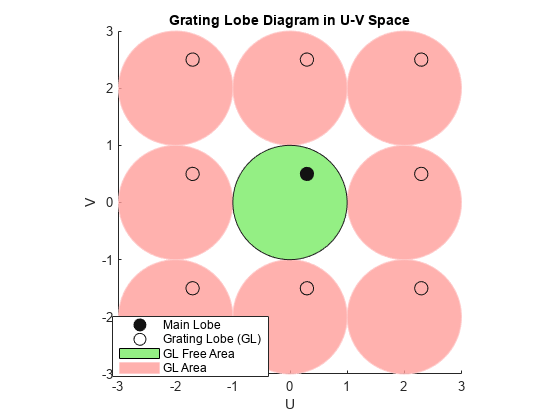
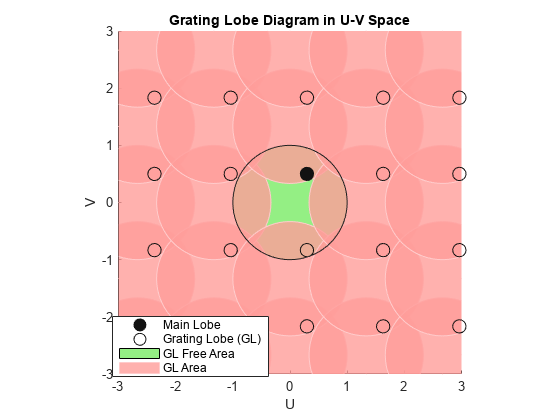
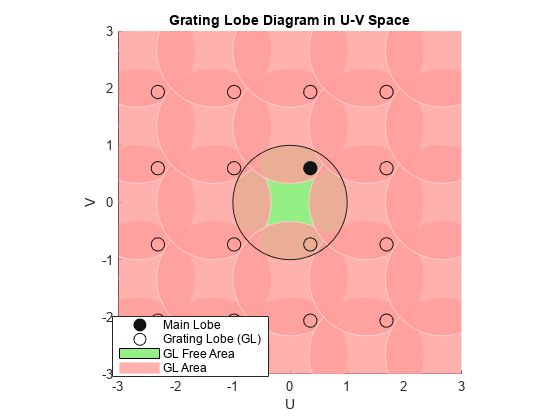
A grating lobe diagram displays the positions of the peaks of the narrowband array pattern. The array pattern depends only upon the geometry of the array and not upon the types of elements which make up the array. Visible and nonvisible grating lobes are displayed as open circles. Only grating lobe peaks near the location of the mainlobe are shown. The mainlobe itself is displayed as a filled circle.
plotGratingLobeDiagram(,
in addition, specifies the array steering angle, H,FREQ,ANGLE)ANGLE.
plotGratingLobeDiagram(,
in addition, specifies the propagation speed by H,FREQ,ANGLE,C)C.
plotGratingLobeDiagram(,
in addition, specifies an array phase-shifter frequency, H,FREQ,ANGLE,C,F0)F0,
that differs from the signal frequency, FREQ.
This argument is useful when the signal no longer satisfies the narrowband
assumption and, allows you to estimate the size of beam squint.
hPlot = plotGratingLobeDiagram(___)
Input Arguments
|
Antenna or microphone array, specified as a System object. |
|
Signal frequency, specified as a scalar. Frequency units are
hertz. Values must lie within a range specified by the frequency property
of the array elements contained in |
|
Array steering angle, specified as either a 2-by-1 vector or
a scalar. If Default: |
|
Signal propagation speed, specified as a scalar. Units are meters per second. Default: Speed of light in vacuum |
|
Phase-shifter frequency of the array, specified as a scalar.
Frequency units are hertz When this argument is omitted, the phase-shifter
frequency is assumed to be the signal frequency, Default: |
Examples
Concepts
Grating Lobes
Spatial undersampling of a wavefield by an array produces visible grating lobes. If you think of the wavenumber, k, as analogous to angular frequency, then you must sample the signal at spatial intervals smaller than π/kmax (or λmin/2) to remove aliasing. The appearance of visible grating lobes is also known as spatial aliasing. The variable kmax is the largest wavenumber value present in the signal.
The directions of maximum spatial response of a URA are determined by the peaks of the
array pattern (alternatively called the beam
pattern or array factor.) Peaks other than
the main lobe peak are called grating lobes. For a URA, the array pattern depends
only on the wavenumber component of the wavefield in the array plane (the
y and z directions for the
phased.URA
System object). The wavenumber components are related to the look-direction of an
arriving wavefield by ky = –2π sin az cos
el/λ and kz = –2π sin el/λ.
The angle az is azimuth angle of the arriving wavefield. The
angle el is elevation angle of the arriving wavefield. The
look-direction points away from the array to the wavefield source.
The array pattern possesses an infinite number of periodically spaced peaks that are equal in strength to the mainlobe peak. If you steer the array to the az0, el0 azimuth and elevation direction, the array pattern for the URA has its mainlobe peak at the wavenumber value, ky0 = –2π sin az0 cos el0/λ, kz0 = –2π sin el0/λ. The array pattern has strong peaks at kym = ky0 + 2π m/dy, kzn = kz0 + 2π n/dz for integer values of m and n. The quantities dy and dz are the inter-element spacings in the y- and z-directions, respectively. Expressed in terms of direction cosines, the grating lobes occur at um = u0 –mλ/dy and vn = v0 –nλ/dz. The main lobe direction cosines are determined by u0 = sin az0 cos el0 and v0 = sin el0 when expressed in terms of the look-direction.
Grating lobes can be visible or nonvisible, depending upon the value of um2 + vn2. When um2 + vn2 ≤ 1, the look direction represents a visible direction. When the value is greater than one, the grating lobe is non-visible. For each visible grating lobe, you can compute a look direction (azm,n,elm,n) from um = sin azm cos elm and vn = sin eln. The spacing of grating lobes depends upon λ/d. When λ/d is small enough, multiple grating lobe peaks can correspond to physical look-directions.
References
[1] Van Trees, H.L. Optimum Array Processing. New York: Wiley-Interscience, 2002.