rotx
Rotation matrix for rotations around x-axis
Syntax
Description
Examples
Rotation Matrix for 30° Rotation
Construct the matrix for a rotation of a vector around the x-axis by 30°. Then let the matrix operate on a vector.
R = rotx(30)
R = 3×3
1.0000 0 0
0 0.8660 -0.5000
0 0.5000 0.8660
x = [2;-2;4]; y = R*x
y = 3×1
2.0000
-3.7321
2.4641
Under a rotation around the x-axis, the x-component of a vector is invariant.
Input Arguments
ang — Rotation angle
real-valued scalar
Rotation angle specified as a real-valued scalar. The rotation angle is positive if the rotation is in the counter-clockwise direction when viewed by an observer looking along the x-axis towards the origin. Angle units are in degrees.
Example: 30.0
Data Types: double
Output Arguments
R — Rotation matrix
real-valued orthogonal matrix
3-by-3 rotation matrix returned as
for a rotation angle α.
More About
Rotation Matrices
Rotation matrices are used to rotate a vector into a new direction.
In transforming vectors in three-dimensional space, rotation matrices are often encountered. Rotation matrices are used in two senses: they can be used to rotate a vector into a new position or they can be used to rotate a coordinate basis (or coordinate system) into a new one. In this case, the vector is left alone but its components in the new basis will be different from those in the original basis. In Euclidean space, there are three basic rotations: one each around the x, y and z axes. Each rotation is specified by an angle of rotation. The rotation angle is defined to be positive for a rotation that is counterclockwise when viewed by an observer looking along the rotation axis towards the origin. Any arbitrary rotation can be composed of a combination of these three (Euler’s rotation theorem). For example, you can rotate a vector in any direction using a sequence of three rotations: .
The rotation matrices that rotate a vector around the x, y, and z-axes are given by:
Counterclockwise rotation around x-axis
Counterclockwise rotation around y-axis
Counterclockwise rotation around z-axis
The following three figures show what positive rotations look like for each rotation axis:
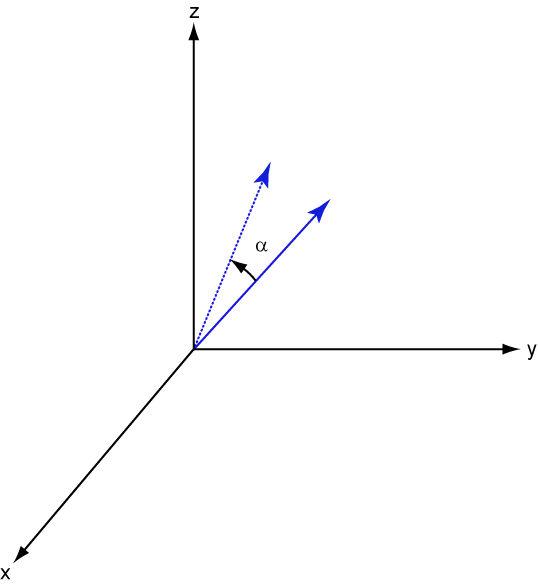
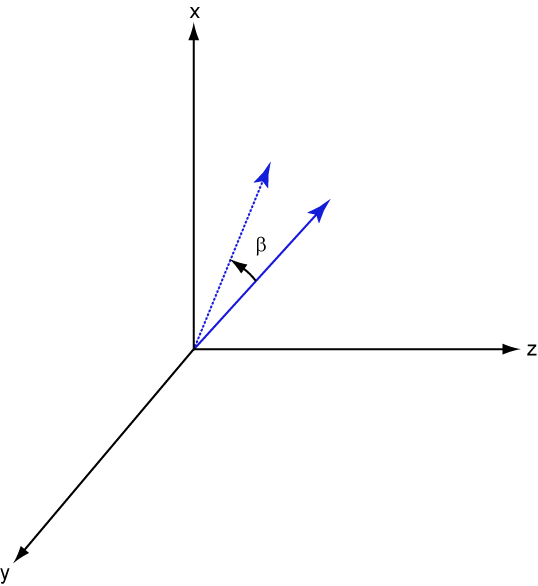
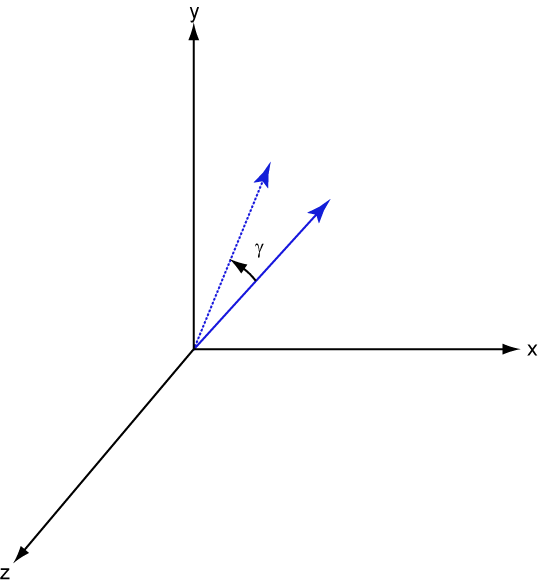
For any rotation, there is an inverse rotation satisfying . For example, the inverse of the x-axis rotation matrix is obtained by changing the sign of the angle:
This example illustrates a basic property: the inverse rotation matrix is the transpose of the original. Rotation matrices satisfy A’A = 1, and consequently det(A) = 1. Under rotations, vector lengths are preserved as well as the angles between vectors.
We can think of rotations in another way. Consider the original set of basis vectors, , and rotate them all using the rotation matrix A. This produces a new set of basis vectors related to the original by:
Using the transpose, you can write the new basis vectors as a linear combinations of the old basis vectors:
Now any vector can be written as a linear combination of either set of basis vectors:
Using algebraic manipulation, you can derive the transformation of components for a fixed vector when the basis (or coordinate system) rotates. This transformation uses the transpose of the rotation matrix.
The next figure illustrates how a vector is transformed as the coordinate system rotates around the x-axis. The figure after shows how this transformation can be interpreted as a rotation of the vector in the opposite direction.
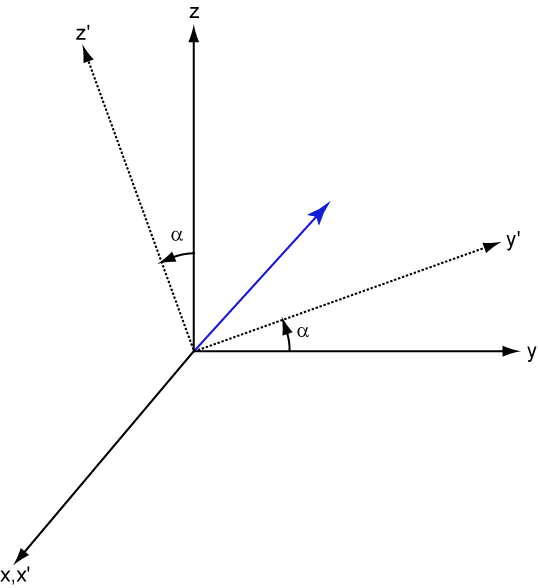
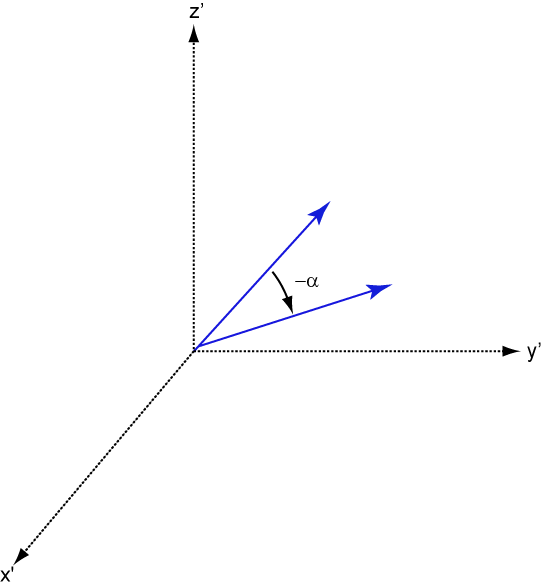
References
[1] Goldstein, H., C. Poole and J. Safko, Classical Mechanics, 3rd Edition, San Francisco: Addison Wesley, 2002, pp. 142–144.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Does not support variable-size inputs.
Version History
Introduced in R2013a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)