Elbow
(To be removed) Hydraulic resistance in elbow
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead. (since R2020a)
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Library
Local Hydraulic Resistances
Description
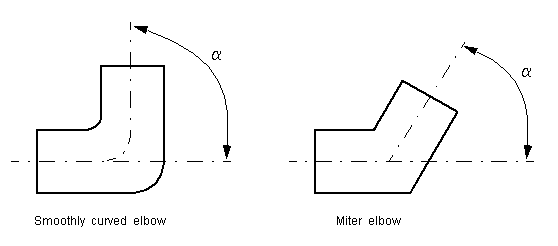
The Elbow block represents an elbow as a local hydraulic resistance. The pressure loss is computed with the semi-empirical formula based on pressure loss coefficient, which is determined in accordance with the Crane Co. recommendations (see [1], p. A-29). Two types of elbow are considered: smoothly curved (standard) and sharp-edged (miter). The block covers elbows in the 5–100 mm and 0–90 degrees range.
The block is based on the Local Resistance block. It computes the pressure loss coefficient and passes its value, as well as the critical Reynolds number value, to the Local Resistance block, which computes the pressure loss according to the formulas explained in the reference documentation for that block.
The pressure loss for turbulent flow regime is determined according to the following formula:
where
q | Flow rate |
p | Pressure loss |
K | Pressure loss coefficient |
A | Elbow cross-sectional area |
| ρ | Fluid density |
The flow regime is checked in the underlying Local Resistance block by comparing the Reynolds number to the specified critical Reynolds number value. For laminar flow regime, the formula for pressure loss computation is modified, as described in the reference documentation for the Local Resistance block.
The core data for the pressure loss coefficient computation is the table-specified
relationship between the friction factor fT and
the internal diameter for clean commercial steel pipes, with flow in the zone of complete
turbulence (see [1], p. A-26). For smoothly curved,
standard 90o elbows, the pressure loss coefficient is determined with
the formula
For elbows with different angles, the coefficient is corrected with the relationship presented in [2], Fig.4.6:
where α is the elbow angle in degrees (0 ≤ α ≤ 90).
Therefore, the pressure loss coefficient for smoothly curved, standard elbows is determined with the formula
For sharp-edged, miter bends the pressure loss coefficient is determined according to the table provided in [1], p. A-29, as a function of the elbow diameter and angle
where 5 ≤ d ≤ 100 mm and 0 ≤ α ≤ 90 degrees.
Connections A and B are conserving hydraulic ports associated with the block inlet and outlet, respectively.
The block positive direction is from port A to port B. This means that the flow rate is positive if fluid flows from A to B, and the pressure differential is determined as .
Warning
The formulas used in the Elbow block are very approximate, especially in the laminar and
transient flow regions. For more accurate results, use the Local Resistance block with a
table-specified K=f(Re) relationship.
Basic Assumptions and Limitations
Fluid inertia is not taken into account.
The elbow is assumed to be made of a clean commercial steel pipe.
Parameters
- Elbow type
The parameter can have one of two values:
Smoothly curvedorSharp-edged (miter). The default value isSmoothly curved.- Elbow internal diameter
The internal diameter of the pipe. The value must be in the range between 5 and 100 mm. The default value is
0.01m.- Elbow angle
The angle of the bend. The value must be in the range between 0 and 90 degrees. The default value is
90deg.- Laminar transition specification
Select how the block transitions between the laminar and turbulent regimes:
Pressure ratio— The transition from laminar to turbulent regime is smooth and depends on the value of the Laminar flow pressure ratio parameter. This method provides better simulation robustness.Reynolds number— The transition from laminar to turbulent regime is assumed to take place when the Reynolds number reaches the value specified by the Critical Reynolds number parameter.
- Laminar flow pressure ratio
Pressure ratio at which the flow transitions between laminar and turbulent regimes. The default value is
0.999. This parameter is visible only if the Laminar transition specification parameter is set toPressure ratio.- Critical Reynolds number
The maximum Reynolds number for laminar flow. The value of the parameter depends on the orifice geometrical profile. You can find recommendations on the parameter value in hydraulics textbooks. The default value is
80. This parameter is visible only if the Laminar transition specification parameter is set toReynolds number.
Global Parameters
Parameters determined by the type of working fluid:
Fluid density
Fluid kinematic viscosity
Use the Hydraulic Fluid block or the Custom Hydraulic Fluid block to specify the fluid properties.
Ports
The block has the following ports:
AHydraulic conserving port associated with the elbow inlet.
BHydraulic conserving port associated with the elbow outlet.
References
[1] Flow of Fluids Through Valves, Fittings, and Pipe, Crane Valves North America, Technical Paper No. 410M
[2] George R. Keller, Hydraulic System Analysis, Published by the Editors of Hydraulics & Pneumatics Magazine, 1970
Extended Capabilities
Version History
Introduced in R2006bSee Also
Gradual Area Change | Local Resistance | Pipe Bend | Sudden Area Change | T-junction