Gate Valve
(To be removed) Hydraulic gate valve
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead. (since R2020a)
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Library
Flow Control Valves
Description
The Gate Valve block models a valve consisting of a round orifice in the valve housing and a flat gate, which moves perpendicular to the orifice axis. The orifice in the gate has the same diameter as the orifice in the housing. As the gate moves, it opens or closes the valve passage (shown as a shaded area in the following illustration).
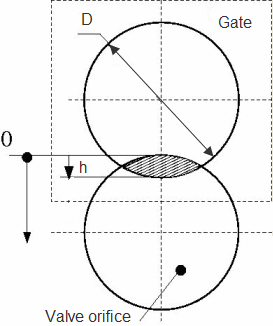
The flow rate through the valve is proportional to the valve opening and to the pressure differential across the valve. The flow rate is determined according to the following equations:
where
| q | Flow rate |
| p | Pressure differential |
| pA, pB | Gauge pressures at the block terminals |
| CD | Flow discharge coefficient |
| A(h) | Instantaneous orifice passage area |
| x0 | Initial opening |
| x | Gate displacement from initial position |
| h | Valve opening |
| D | Orifice diameter |
| ρ | Fluid density |
| Aleak | Closed valve leakage area |
| pcr | Minimum pressure for turbulent flow |
The minimum pressure for turbulent flow, pcr, is calculated according to the laminar transition specification method:
By pressure ratio — The transition from laminar to turbulent regime is defined by the following equations:
pcr = (pavg + patm)(1 – Blam)
pavg = (pA + pB)/2
where
pavg Average pressure between the block terminals patm Atmospheric pressure, 101325 Pa Blam Pressure ratio at the transition between laminar and turbulent regimes (Laminar flow pressure ratio parameter value) By Reynolds number — The transition from laminar to turbulent regime is defined by the following equations:
where
DH Valve instantaneous hydraulic diameter ν Fluid kinematic viscosity Recr Critical Reynolds number (Critical Reynolds number parameter value)
Connections A and B are hydraulic conserving ports. Connection S is a physical signal
port that controls the gate displacement. The block positive direction is from port A to
port B. This means that the flow rate is positive if it flows from A to B, and the
pressure differential is determined as . Positive signal at the physical signal port S
opens the valve.
Basic Assumptions and Limitations
No inertial effects are taken into account.
Parameters
- Valve orifice diameter
The diameter of the valve orifice. The orifices in the valve housing and in the gate have the same diameter. The default value is
0.01m.- Initial opening
The initial opening of the valve. The parameter can take both positive and negative values. The default value is
0.- Flow discharge coefficient
Semi-empirical parameter for valve capacity characterization. Its value depends on the geometrical properties of the orifice, and usually is provided in textbooks or manufacturer data sheets. The default value is
0.65.- Laminar transition specification
Select how the block transitions between the laminar and turbulent regimes:
Pressure ratio— The transition from laminar to turbulent regime is smooth and depends on the value of the Laminar flow pressure ratio parameter. This method provides better simulation robustness.Reynolds number— The transition from laminar to turbulent regime is assumed to take place when the Reynolds number reaches the value specified by the Critical Reynolds number parameter.
- Laminar flow pressure ratio
Pressure ratio at which the flow transitions between laminar and turbulent regimes. The default value is
0.999. This parameter is visible only if the Laminar transition specification parameter is set toPressure ratio.- Critical Reynolds number
The maximum Reynolds number for laminar flow. The value of the parameter depends on the orifice geometrical profile. You can find recommendations on the parameter value in hydraulics textbooks. The default value is
10. This parameter is visible only if the Laminar transition specification parameter is set toReynolds number.- Leakage area
The total area of possible leaks in the completely closed valve. The main purpose of the parameter is to maintain numerical integrity of the circuit by preventing a portion of the system from getting isolated after the valve is completely closed. The parameter value must be greater than 0. The default value is
1e-12m^2.
Global Parameters
Parameters determined by the type of working fluid:
Fluid density
Fluid kinematic viscosity
Use the Hydraulic Fluid block or the Custom Hydraulic Fluid block to specify the fluid properties.
Ports
The block has the following ports:
AHydraulic conserving port associated with the valve inlet.
BHydraulic conserving port associated with the valve outlet.
SPhysical signal port that controls the gate displacement. The signal applied to this port is treated as translational motion, in meters.

