Torque Converter
Viscous fluid coupling between rotating driveline shafts
Libraries:
Simscape /
Driveline /
Couplings & Drives
Description
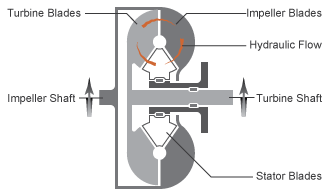
The Torque Converter block models a torque converter. The Torque Converter block has two mechanical rotational conserving ports that are associated with the impeller and turbine, respectively. The block transfers torque and angular velocity between the impeller port I and turbine port T by acting as a lookup table. The block can simulate drive (power flows from I port to T port) and coast (power flows from T port to I port) modes.
Examples
Limitations
When Coast mode modeling is set to
Continuous:
The impeller shaft must always rotate in a positive direction. Simulation is not valid for < 0.
If you drive the Torque Converter block by using a torque source, such as the Generic Engine block, you must include an inertia in the source to represent the engine, shaft inertia, or other source components. To ensure that the impeller starts by rotating in a positive direction, set the initial speed for this inertia to a positive value.
Ports
Conserving
I — Impeller
mechanical rotational
Mechanical rotational conserving port associated with the impeller.
T — Turbine
mechanical rotational
Mechanical rotational conserving port associated with turbine.
Parameters
Torque Characteristics
Coast mode modeling — Modeling type of torque converter
Two-mode (default) | Continuous
Modeling type of the torque converter specified as either
Two-mode or Continuous. The
Continuous modeling type supports both drive and coast
modes but has reduced accuracy and robustness when modeling near the transition
between coasting and driving modes. Therefore, if the simulation involves a coast
mode, use the Two-mode modeling type due to its better
robustness and accuracy when modeling the coast mode.
Drive mode speed ratio vector — Turbine speed to impeller speed ratios
[0, .5, .6, .7, .8, .87, .92, .94, .96, .97, 1] (default) | vector
Speed ratios, , of the drive mode. The vector elements must be in ascending order starting at 0 and ending at 1.
Dependencies
To enable this parameter, set Coast mode modeling to
Two-mode.
Drive mode torque ratio vector — Turbine torque to impeller torque ratios
[2.232, 1.5462, 1.4058, 1.2746, 1.1528, 1.0732, 1.0192, 1, 1, 1,
1] (default) | vector
Torque ratios, , of the drive mode. Each element of the vector must be greater than or equal to 1, and the last element must be 1.
Dependencies
To enable this parameter, set Coast mode modeling to
Two-mode.
Drive mode capacity factor vector — Capacity factors of drive mode
1e-4 * [.72558, .66322, .63463, .59042, .51331, .4144, .29287,
.22444, .12186, .04386, 0] m*N/rpm^2 (default) | vector
Capacity factors,, of the drive mode. Each element of the vector must be nonnegative, and the last element must be 0.
Dependencies
To enable this parameter, set Coast mode modeling to
Two-mode.
Coast mode speed ratio vector — Impeller speed to turbine speed ratios
[0, .5, .6, .7, .8, .87, .92, .94, .96, .97, 1] (default) | vector
Speed ratios, , of the coast mode. The vector elements must be in ascending order starting at 0 and ending at 1.
Dependencies
To enable this parameter, set Coast mode modeling to
Two-mode.
Coast mode capacity factor vector — Capacity factors of coast mode
1e-4 * [.5079, .4643, .4442, .4133, .3593, .2901, .205, .1571,
.0853, .0307, 0] m*N/rpm^2 (default) | vector
Capacity factors, , of the coast mode. Each element of the vector must be nonnegative, and the last element must be 0.
Dependencies
To enable this parameter, set Coast mode modeling to
Two-mode.
Interpolation method — Interpolation method of lookup function
Linear (default) | Smooth
Interpolation method of the lookup function, specified as either
Linear or Smooth. The method
interpolates torque ratio and capacity factor functions between the discrete relative
velocity values within the definition range. For more information about
Linear and Smooth, see tablelookup.
Extrapolation method — Extrapolation method of lookup function
Linear (default) | Nearest | Error
Extrapolation method of the lookup function, specified as
Linear, Smooth, or
Error. The method extrapolates torque ratio and capacity
factor functions. For more information about Linear,
Smooth, and Error, see tablelookup.
Initial mode — Initial mode of simulation
Drive mode (default) | Coast mode
Initial mode of the simulation, specified as either Drive
mode or Coast mode.
Mode transition threshold — Threshold of mode transition
1 rpm (default) | positive scalar
Mode transition threshold of the simulation. Setting a threshold for the mode transition can increase the simulation robustness by avoiding the high frequency mode switching.
Dependencies
To enable this parameter, set Coast mode modeling to
Two-mode.
Speed ratio vector — Turbine speed to impeller speed ratios
[0, .5, .6, .7, .8, .87, .92, .94, .96, .97] (default) | vector
Speed ratios, , of the torque converter. Each element of the vector must be in ascending order and in the range [0,1].
Dependencies
To enable this parameter, set Coast mode modeling to
Continuous.
Torque ratio vector — Turbine torque to impeller torque ratios
[2.232, 1.5462, 1.4058, 1.2746, 1.1528, 1.0732, 1.0192, .9983,
.9983, .9983, .9983] (default) | vector
Torque ratios, , of the torque converter. Each element of the vector must be positive.
Dependencies
To enable this parameter, set Coast mode modeling to
Continuous.
Capacity factor parameterization — Definition of capacity factor
Ratio of speed to square root of impeller
torque (default) | Ratio of impeller torque to square of speed
Definition of the capacity factor of the converter, defined as either
Ratio of speed to square root of impeller torque or
Ratio of impeller torque to square of speed. The setting
of this parameter affects the Capacity factor vector.
For
Ratio of speed to square root of impeller torqueparameter:For
Ratio of impeller torque to square of speedparameter:
Dependencies
To enable this parameter, set Coast mode modeling to
Continuous.
Capacity factor reference speed — Choice of speed for capacity factor definition
Always impeller speed (default) | Turbine speed for speed ratios greater than
one
Choice of speed for the capacity factor definition, specified as either
Always impeller speed or Turbine speed for
speed ratios greater than one.
Always impeller speed: Use impeller speed for all values of .Turbine speed for speed ratios greater than one: Use impeller speed for all values of < 1, and use turbine speed when > 1.
Dependencies
To enable this parameter, set Coast mode modeling to
Continuous.
Capacity factor vector — Capacity factors
[12.2938, 12.8588, 13.1452, 13.6285, 14.6163, 16.2675, 19.3503,
22.1046, 29.9986, 50] (rad/s)/(N*m)^0.5 (default) | vector
Capacity factors of the converter. You can define the capacity factor as:
Capacity factor
|
| Set Capacity factor parameterization parameter to
Ratio of speed to square root of impeller
torque. |
|
| Set Capacity factor parameterization parameter to
Ratio of impeller torque to the square of the
speed. The default value is 1e-3 * [6.616, 6.048, 5.787,
5.384, 4.681, 3.779, 2.671, 2.047, 1.111, .4]
N*m/(rad/s)^2. |
Note
If you do not specify capacity factor data for a speed ratio of 1, the block uses a capacity factor value of 10*KMax, where KMax is the maximum value in the specified capacity factor vector. The corresponding torque ratio is assumed to be 0. For all other speed ratio values not explicitly specified in the lookup table data, the block uses the interpolation or extrapolation method selected in the block property inspector.
Dependencies
To enable this parameter, set Coast mode modeling to
Continuous.
Dynamics
To enable the Dynamics, set the Coast mode
modeling parameter to Continuous.
Model transmission lag — Transmission lag setting
No lag – Suitable for HIL
simulation (default) | Specify time constant and initial value
Transmission lag setting, specified as either No lag – Suitable for
HIL simulation or Specify time constant and initial
value.
No lag – Suitable for HIL simulation: Torque transfer is instantaneous.When there is no time lag, the input impeller torque, , and output turbine torque, , are:
Specify time constant and initial value: Torque is transferred with a time lag. If you select this option, you can specify the Torque transmission time constant and Initial turbine-to-impeller torque ratio parameters.Note
For optimal simulation performance, select
No lag - Suitable for HIL simulation.
Torque transmission time constant — Time constant of torque transmission
.02 s (default) | positive scalar
Torque transmission time. The time lag increases model fidelity but reduces simulation performance. See Adjust Model Fidelity for more information.
Dependencies
To enable this parameter, set Model transmission lag to
Specify time constant and initial value.
Initial turbine-to-impeller torque ratio — Initial torque ratio of turbine to impeller
0 (default) | positive scalar
Initial torque ratio of the turbine to the impeller.
You can optionally include the effect of torque transmission time lag that is caused by internal fluid flow and compressibility. Instead of and being instantaneously constrained to one another, a first-order time lag introduces a delayed response in the impeller torque:
The preceding instantaneous function of the capacity factor K determines the steady-state value of τI.
Dependencies
To enable this parameter, set Model transmission lag to
Specify time constant and initial value.
References
[1] Society of Automotive Engineers, Hydrodynamic Drive Test Code (Surface Vehicle Recommended Practice), SAE J643, Dec 2018.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2011a
See Also
Simscape Blocks
Topics
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)



