Spline
Cubic interpolating plane curve or space curve
Libraries:
Simscape /
Multibody /
Curves and Surfaces
Description
This Spline block creates a continuous spline curve based on cubic interpolation between the specified points. The curve can be two dimensional, such as a planar cam profile, or three dimensional, such as a roller coaster track. The dimension of the spline depends on the dimension of the coordinate matrix. An N-by-2 matrix specifies a 2-D curve in the xy plane. An N-by-3 matrix specifies a 3-D curve. All the coordinates are resolved in the local reference frame of the block. Moreover, according to the specified end conditions, the curve can be either open or closed.
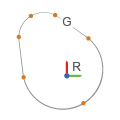
Ports
Frame
R — Reference frame
frame
Spline curve reference frame. Connect this frame port to another block to specify the location and orientation of the spline curve in a model.
Geometry
G — Spline curve representation
geometry
Geometry data associated with the representation of a 2-D or 3-D continuous spline curve. It provides the spline curve specification to other blocks to which it connects, such as the Point on Curve Constraint block.
Parameters
Interpolation Points — Coordinates of interpolation points for specifying spline curve
[6 -2 9; -6 5 -4; -6 -7 9; 6 0 -4; -3 6 9; -3 -8 -4]
m (default) | N-by-2 matrix | N-by-3 matrix
Matrix that includes the coordinates of the interpolation points for defining the spline curve. Use an N-by-2 matrix to specify a 2-D spline and an N-by-2 matrix to specify a 3-D spline. Each row of the matrix specifies the Cartesian coordinates of an interpolation point with respect to the reference frame of the Spline block. An error occurs if the matrix has any repeated rows.
Tips
You can use the unique function to
remove repeated rows from an input matrix.
End Conditions — Treatment of the curve endpoints
Periodic (Closed) (default) | Natural (Open)
End conditions of the spline curve. The Periodic
(Closed) end conditions correspond to a closed curve. For
this condition, the block joins the first and last data points with a
continuous curve. The Natural (Open) end
condition corresponds to an open curve.
The spline curve is a piecewise function of third-order polynomial segments connected end-to-end. The curve is built such that adjacent polynomial segments have the same first and second derivatives at the shared endpoints.
Type — Spline visualization setting
From Geometry (default) | Marker | None
Visualization setting for this spline. Use the default setting,
From Geometry, to show the spline. Select
Marker to show a graphic marker such as a
sphere or frame. Select None to disable
visualization for this spline.
Visual Properties — Parameterizations for color and opacity
Simple (default) | Advanced
Parameterizations for specifying visual properties. Select
Simple to specify Diffuse
Color and Opacity. Select
Advanced to specify more visual
properties, such as Specular Color, Ambient
Color, Emissive Color, and
Shininess.
Dependencies
To enable this parameter, set Type to From
Geometry or
Marker.
Diffuse Color — True color as [R,G,B,A]
[0.0 0.0 0.0] (default) | three-element vector | four-element vector
True color under direct white light, specified as an [R,G,B] or [R,G,B,A] vector on a 0–1 scale. An optional fourth element specifies the color opacity on a scale of 0–1. Omitting the opacity element is equivalent to specifying a value of 1.
Dependencies
To enable this parameter, set Type to
From Geometry or
Marker.
Opacity — Graphic opacity
1.0 (default) | scalar in the range of 0 to 1
Graphic opacity, specified as a scalar in the range of 0 to 1. A scalar of 0 corresponds to completely transparent, and a scalar of 1 corresponds to completely opaque.
Dependencies
To enable this parameter, set:
Type to
From GeometryorMarkerVisual Properties to
Simple
Specular Color — Color of light due to specular reflection
[0.5 0.5 0.5 1.0] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1 | 4-by-1 or 1-by-4 vector with values in the range of 0 to 1
Color of the light due to specular reflection, specified as an [R,G,B] or [R,G,B,A] vector with values in the range of 0 to 1. The vector can be a row or column vector. The optional fourth element specifies the color opacity. Omitting the opacity element is equivalent to specifying a value of 1. This parameter changes the color of the specular highlight, which is the bright spot on the rendered solid due to the reflection of the light from the light source.
Dependencies
To enable this parameter, set:
Type to
From GeometryorMarkerVisual Properties to
Advanced
Ambient Color — Color of ambient light
[0.15 0.15 0.15 1.0] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1 | 4-by-1 or 1-by-4 vector with values in the range of 0 to 1
Color of the ambient light, specified as an [R,G,B] or [R,G,B,A] vector with values in the range of 0 to 1. The vector can be a row or column vector. The optional fourth element specifies the color opacity. Omitting the opacity element is equivalent to specifying a value of 1.
Ambient light refers to a general level of illumination that does not come directly from a light source. The Ambient light consists of light that has been reflected and re-reflected so many times that it is no longer coming from any particular direction. You can adjust this parameter to change the shadow color of the rendered solid.
Dependencies
To enable this parameter, set:
Type to
From GeometryorMarkerVisual Properties to
Advanced
Emissive Color — Self-illumination color
[0.0 0.0 0.0 1.0] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1
Color due to self illumination, specified as an [R,G,B] or [R,G,B,A] vector in the range of 0 to 1. The vector can be a row or column vector. The optional fourth element specifies the color opacity. Omitting the opacity element is equivalent to specifying a value of 1.
The emission color is color that does not come from any external source, and therefore seems to be emitted by the solid itself. When a solid has a emissive color, the solid can be seen even if there is no external light source.
Dependencies
To enable this parameter, set:
Type to
From GeometryorMarkerVisual Properties to
Advanced
Shininess — Highlight sharpness
75 (default) | scalar with value constrained to 0–128
Sharpness of specular light reflections, specified as a scalar number on a 0–128 scale. Increase the shininess value for smaller but sharper highlights. Decrease the value for larger but smoother highlights.
Dependencies
To enable this parameter, set:
Type to
From GeometryorMarkerVisual Properties to
Advanced
Shape — Shape of graphic marker
Sphere (default) | Cube | Frame
Geometrical shape of the graphic marker. The Mechanics Explorer shows the marker using the selected shape.
Dependencies
To enable this parameter, set Type to
Marker.
Size — Width of the marker in pixels
10 pixels (default) | scalar
Width of the marker in pixels. This width does not scale with zoom level. Note that the apparent size of the marker depends partly on screen resolution, with higher resolutions packing more pixels per unit length, and therefore producing smaller icons.
Dependencies
To enable this parameter, set Type to Marker.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2015b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

