Grounding Transformer
Implement three-phase grounding transformer providing a neutral in three-wire system
Library
Simscape / Electrical / Specialized Power Systems / Power Grid Elements
Description
Grounding transformers are used in utility distribution networks and in some power electronic converters in order to provide a neutral point in a three-wire system. This transformer is a three-phase two-winding transformer with winding 1 and winding 2 connected in zig zag as shown in the figure below.
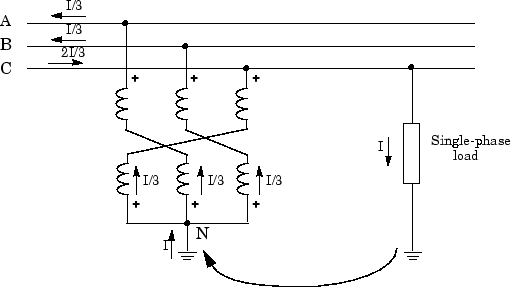
The figure shows a single-phase load connected between phase C and ground in a three-wire system. The current I absorbed by the load returns to the source through the ground and the neutral of the grounding transformer. Because of the zig zag connection and the opposite winding polarities of upper and lower windings, the grounding transformer offers a low impedance in zero-sequence while keeping a very high impedance to positive-sequence. In other words, only a zero-sequence current can flow through the three windings. By definition, a zero-sequence current is a set of three-phase currents having same magnitude and phase. Therefore, the neutral current I shares into three equal currents I/3. Because the three currents flowing in the grounding transformer are equal, the neutral point stays fixed and the line-to-neutral voltages remain balanced.
The grounding transformer is modeled by three two-winding transformers having a 1:1 voltage ratio. Assume six identical windings with:
R = winding resistances
X =
winding leakage reactances
Rmag,
Xmag= parallel resistance and reactance of the magnetizing branch
The positive-sequence impedance Z1 and the zero-sequence impedance Z0 of the grounding transformer are given by:
The zero-sequence reactance X0 is the most important parameter of the grounding transformer. In order to minimize voltage unbalance, reactance X0 should be kept as low as possible.
Parameters
- Units
Specify the units used to enter the parameters of the Grounding Transformer block. Select
puto use per unit. SelectSIto use SI units. Changing the Units parameter fromputoSI, or fromSItopu, will automatically convert the parameters displayed in the mask of the block. The per unit conversion is based on the transformer rated power Pn in VA, nominal frequency fn in Hz, and nominal voltage Vn, in Vrms, of the windings. Default ispu.- Nominal power and frequency
The nominal power rating, in volt-amperes (VA), and nominal frequency, in hertz (Hz), of the transformer. Note that the nominal parameters have no impact on the transformer model when the Units parameter is set to
SI. Default is[100e6 60].- Nominal voltage
The nominal phase-to-phase voltage Vn of the Grounding Transformer, in volts RMS (Vrms). Default is
25e3.- Zero-sequence resistance and reactance
The zero-sequence resistance R0 and the zero-sequence reactance X0 in pu or in ohms. Default is
[0.025 0.75]when the Units parameter ispuand[0.15625 4.6875]when the Units parameter isSI.- Magnetization branch
The shunt resistance Rm modeling the transformer core losses and the magnetizing reactance Xm modeling the magnetization current, in pu or ohms. Default is
[500 500]when the Units parameter ispuand[3125 3125]when the Units parameter isSI.These values define the active power losses P and the reactive power losses Q required for magnetizing the grounding transformer.
As the nominal voltage across each of the six windings is the nominal line-to-line voltage divided by 3 (Vn/3), the three impedances effectively connected across one of the two windings on each leg are Rmag=Rm/3 and Xmag=Xm/3.
- Measurements
Select
Voltagesto measure the line-to-neutral voltages at the terminals of the Grounding Transformer block.Select
Currentsto measure the currents flowing into the three terminals of the Grounding Transformer block.Select
All voltages and currentsto measure voltages and currents.Default is
None.Place a Multimeter block in your model to display the selected measurements during the simulation. In the Available Measurements list box of the Multimeter block, the measurements are identified by a label followed by the block name.
Measurement
Label
line-to-neutral voltages
Uancurrents
Ian
Limitations
Saturation of the grounding transformer is not modeled.
See Also
Linear Transformer, Multimeter, Three-Phase Transformer (Two Windings), Three-Phase Transformer (Three Windings)
Version History
Introduced in R2008a
