Mechanical Shaft
Implement mechanical shaft
Description
The model outputs the transmitted torque through the shaft regarding the speed difference between the driving side and the loaded side of the shaft.
The transmitted torque Tl is given by the following equation:
where K (N.m) is the shaft stiffness, B (N.m.s) is the internal damping, and ωm and ωl are the speeds (rad/s) of the driving side and the loaded side, respectively. The following figure shows the internal schematic of the model. In this model the speeds are converted from rpm to rad/s.
Mechanical Shaft Model Schematic
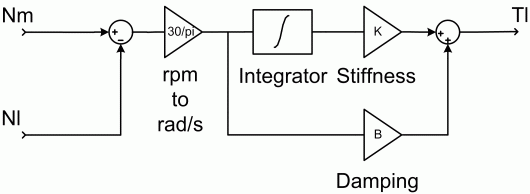
The stiffness is defined as
K = T / θ,
where T is the torsional torque applied to the shaft and θ the resulting angular deflection (rad).
The stiffness can also be determined by
K = GJ / l,
where G is the shear modulus, J the polar moment of inertia, and l the length of the shaft.
For steel, the shear modulus G is usually equal to about 80 GPa, and the polar moment of inertia J of a shaft with a circular section of diameter D is given by
J = πD4 / 32.
Mechanical shafts have very small angular deflections to avoid bearing problems. As an example, the following table gives the corresponding stiffness for angular deflections of 0.1 degrees at maximum torque with respect to the power and speed of electrical motors connected to the driving end of the shaft. The maximum torque is here assumed to be 1.5 times bigger than the nominal torque.
Shaft Stiffness K
P (HP) | N (rpm) | T (N.m) | Tmax (N.m) (=1.5 T) | K (N.m) |
|---|---|---|---|---|
5 | 1750 | 20 | 30 | 17190 |
200 | 1750 | 815 | 1223 | 700730 |
200 | 1200 | 1190 | 1785 | 1022730 |
The damping factor B represents internal friction. This factor increases with the shaft stiffness. As an example, the following table gives some values of B for the stiffness of the preceding table.
Shaft Internal Damping B
K (N.m) | B (N.m.s) |
|---|---|
17190 | 600 |
700730 | 24460 |
1022730 | 35700 |
Simulink Schematic
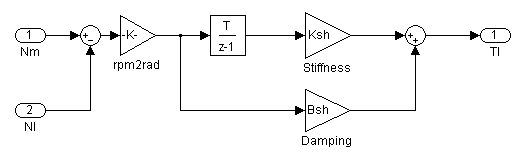
Remarks
The stiffness must be high enough to avoid large angular deflections that could cause misalignment inside the bearings and damage.
For proper simulation results, the internal damping must be high enough to avoid undesired transient speed and torque oscillations.
The model is discrete. Good simulation results have been obtained with a 10-µs time step.
Parameters
- Preset model
This pop-up menu allows you to choose preset model parameters. When you select a preset model, the other block parameters become inaccessible. Default is
No.- Stiffness
The stiffness of the shaft (N.m). Default is
17190.- Damping
The internal damping of the shaft (N.m.s). Default is
600.
Block Inputs and Outputs
Inputs
The block has two inputs: Nm and Nl.
The first input, Nm, is the speed (rpm) of the driving end of the shaft.
The second input, Nl, is the speed (rpm) of the load connected to the second end of the shaft.
Outputs
The block has one output: Tl.
The Tl output is the torque transmitted from the driving end of the shaft to the load.
Model Specifications
The library contains three preset models. The nominal torques of these mechanical shaft models are shown in the following table:
Preset Mechanical Shaft Models
1st | 2nd | 3rd | |
Nominal torque (N.m) | 20 | 815 | 1190 |
The preset models have been designed in order to present 0.1 degrees of angular deflection at maximum torque (supposed to be 1.5 times the nominal torque).
References
[1] Norton, Robert L., Machine Design, Prentice Hall, 1998.
[2] Nise, Norman S., Control Systems Engineering, Addison-Wesley Publishing Company, 1995.
Version History
Introduced in R2006a
