PLL (3ph)
Determine frequency and fundamental component of three-phase signal phase angle
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Control
Description
The PLL (3ph) block models a Phase Lock Loop (PLL) closed-loop control system, which tracks the frequency and phase of a sinusoidal three-phase signal by using an internal frequency oscillator. The control system adjusts the internal oscillator frequency to keep the phases difference to 0.
The figure shows the internal diagram of the PLL.
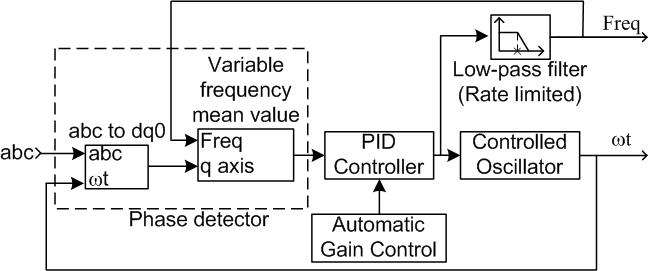
The three-phase input signal is converted to a dq0 rotating frame (Park transform) using the angular speed of an internal oscillator. The quadrature axis of the signal, proportional to the phase difference between the abc signal and the internal oscillator rotating frame, is filtered with a Mean (Variable Frequency) block. A Proportional-Integral-Derivative (PID) controller, with an optional automatic gain control (AGC), keeps the phase difference to 0 by acting on a controlled oscillator. The PID output, corresponding to the angular velocity, is filtered and converted to the frequency, in hertz, which is used by the mean value.
Characteristics
| Sample Time | Specified in the Sample Time
parameter. Continuous when Sample Time = 0. |
| Scalar Expansion | No |
| Dimensionalized | No |
| Zero-Crossing Detection | Yes |
Examples
The power_PLL example shows the use of the PLL (3ph) and PLL
blocks.
The PLL block is fed by a sinusoidal signal of 60 Hz, increasing to 61 Hz from 0.5 s to 1.5 s. Notice that the frequency reaches the new frequency in a short response time.
The PLL (3ph) block is fed by three-phase sinusoidal signals increasing from 60 Hz to 61 Hz between 0.5 and 1.5 seconds. The PLL (3ph) frequency reaches the new frequency faster than the PLL due to the additional phase information.
The model sample time is parameterized with the variable Ts (with a default value of 0). To discretize the PLL block, at the MATLAB® command prompt, enter
Ts = 50e-6
Ports
Input
Output
Parameters
Extended Capabilities
Version History
Introduced in R2013a
