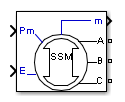
Simplified Synchronous Machine
Model the dynamics of simplified three-phase synchronous machine
Libraries:
Simscape /
Electrical /
Electromechanical /
Synchronous
Description
The Simplified Synchronous Machine block models both the electrical and mechanical characteristics of a simple synchronous machine.
The electrical system for each phase consists of a voltage source in series with an RL impedance, which implements the internal impedance of the machine. The value of R can be zero but the value of L must be positive.
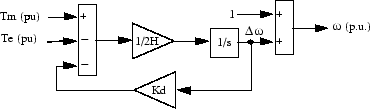
The Simplified Synchronous Machine block implements the mechanical system described by
where
| Δω = Speed variation with respect to speed of
operation H = constant of inertia Tm = mechanical torque Te = electromagnetic torque Kd = damping factor representing the effect of damper windings ω(t) = mechanical speed of the rotor ω0 = speed of operation (1 p.u.) | (1) |
Although the parameters can be entered in either SI units or per unit in the dialog box, the internal calculations are done in per unit. The following block diagram illustrates how the mechanical part of the model is implemented. The model computes a deviation with respect to the speed of operation; not the absolute speed itself.
The Kd damping coefficient simulates the effect of damper windings normally used in synchronous machines. When the machine is connected to an infinite network (zero impedance), the variation of machine power angle delta (δ) resulting from a change of mechanical power (Pm) can be approximated by the following second-order transfer function:
where
δ | Power angle delta: angle of internal voltage E with respect to terminal voltage, in radians |
Pm | Mechanical power in pu |
ωn | Frequency of electromechanical oscillations = in rad/s |
ζ | Damping ratio = |
ωs | Electrical frequency in rad/s |
Pmax | Maximum power in pu transmitted through reactance X at terminal voltage Vt and internal voltage E. Pmax = VtE/X, where Vt, E, and X are in pu |
H | Inertia constant(s) |
Kd | Damping factor (pu_of_torque / pu_of_speed) |
This approximate transfer function, which has been derived by assuming sin(δ) = δ, is valid for small power angles (δ < 30 degrees). It follows from the preceding ζ expression that the Kd value required to obtain a given ζ damping ratio:
Examples
The power_simplealt
example uses the Simplified Synchronous Machine block to represent a 1000
MVA, 315 kV, 60 Hz equivalent source connected to an infinite bus (Three-Phase Programmable
Voltage Source block). The Simplified Synchronous Machine (SI Units) block is used as a
synchronous generator. The internal resistance and reactance are set respectively to 0.02 pu
(1.9845 Ω) and 0.2 pu (X = 19.845 Ω; L = 0.0526 H). The inertia of the machine is J =
168,870 kg.m2, corresponding to an inertia constant H = 3 s. The
electrical frequency is ωs = 2*π*60 = 377 rad/s. The machine has two
pairs of poles such that its synchronous speed is 2*π*60/2 = 188.5 rad/s or 1800 rpm.
The Load Flow option of the Powergui has been used to initialize the machine to start simulation in steady state with the machine generating 500 MW. The required internal voltage computed by the load flow is 1.0149 pu. Therefore, an internal voltage E = 315e3*1.0149 = 319,690 Vrms phase-to-phase is specified in the Constant block connected to the E input. The maximum power that can be delivered by the machine with a terminal voltage Vt = 1.0 pu and an internal voltage E = 1.0149 pu is Pmax = Vt*E/X = 1.0149/0.2 = 5.0745 pu.
The damping factor Kd is adjusted to obtain a damping ratio ζ = 0.3. The required Kd value is:
Two Fourier blocks measure the power angle δ. This angle is computed as the difference between the phase angle of phase A internal voltage and the phase angle of phase A terminal voltage.
In this example, a step is performed on the mechanical power applied to the shaft. The machine is initially running in steady state with a mechanical power of 505 MW (mechanical power required for an output electrical power of 500 MW, considering the resistive losses). At t = 0.5 s the mechanical power is suddenly increased to 1000 MW.
Run the example and observe the electromechanical transient on the Scope block displaying the power angle δ in degrees, the machine speed in rpm, and the electrical power in MW.
For an initial electrical power Pe = 500 MW (0.5 pu), the load angle δ is 5.65 degrees, which corresponds to the expected value:
As the mechanical power is stepped from 0.5 pu to 1.0 pu, the load angle increases and goes through a series of under damped oscillations (damping ratio ζ = 0.3) before stabilizing to its new value of 11.3 degrees. The frequency of the oscillations is given by:
Assumptions and Limitations
The electrical system of the Simplified Synchronous Machine block consists solely of a voltage source behind a synchronous reactance and resistance. All the other self- and magnetizing inductances of the armature, field, and damping windings are neglected. The effect of damper windings is approximated by the damping factor Kd. The three voltage sources and RL impedance branches are Y-connected (three wires or four wires). The load might or might not be balanced.
When you use Simplified Synchronous Machine blocks in discrete systems, you might have to use a small parasitic resistive load, connected at the machine terminals, to avoid numerical oscillations. Large sample times require larger loads. The minimum resistive load is proportional to the sample time. Remember that with a 25 μs time step on a 60 Hz system, the minimum load is approximately 2.5% of the machine nominal power. For example, a 200 MVA simplified synchronous machine in a power system discretized with a 50 μs sample time requires approximately 5% of resistive load or 10 MW. If the sample time is reduced to 20 μs, a resistive load of 4 MW should be sufficient.
Ports
Input
Output
Conserving
Parameters
Extended Capabilities
Version History
Introduced before R2006a