VSC-Based HVDC Link
Introduction
The increasing rating and improved performance of self-commutated semiconductor devices have made possible High Voltage DC (HVDC) transmission based on Voltage-Sourced Converter (VSC). Two technologies offered by the manufacturers are the HVDC Light [1] and the HVDCplus [2].
The example described in this section illustrates modeling of a forced-commutated Voltage-Sourced Converter high-voltage direct current (VSC-HVDC) transmission link. The objectives of this example are to demonstrate the use of Simscape™ Electrical™ Specialized Power Systems blocks in the simulation of a HVDC transmission link based on three-level Neutral Point Clamped (NPC) VSC converters with single-phase carrier based Sinusoidal Pulse Width Modulation (SPWM) switching. Perturbations are applied to examine the system dynamic performance.
Description of the HVDC Link
The principal characteristic of VSC-HVDC transmission is its ability to independently control the reactive and real power flow at each of the AC systems to which it is connected, at the Point of Common Coupling (PCC). In contrast to line-commutated HVDC transmission, the polarity of the DC link voltage remains the same with the DC current being reversed to change the direction of power flow.
The HVDC link described in this example is available in the
power_hvdc_vsc model. You can run the command by entering
the following in the MATLAB® Command Window: power_hvdc_vsc. Load this model and
save it in your working directory as case5 to allow further
modifications to the original system. This model represents a 200 MVA, +/- 100 kV
VSC-HVDC transmission link.
The 230 kV, 2000 MVA AC systems (AC system1 and AC system2 subsystems) are modeled by damped L-R equivalents with an angle of 80 degrees at fundamental frequency (50 Hz) and at the third harmonic. The VSC converters are three-level bridge blocks using IGBT/diodes. The relative ease with which the IGBT can be controlled and its suitability for high-frequency switching, has made this device the better choice over GTO and thyristors. Open the Station 1 and Station 2 subsystems to see how they are built.
A converter transformer (Wye grounded /Delta) is used to permit the optimal voltage transformation. The present winding arrangement blocks tripplen harmonics produced by the converter. The transformer tap changer or saturation are not simulated. The tap position is rather at a fixed position determined by a multiplication factor applied to the primary nominal voltage of the converter transformers The multiplication factors are chosen to have a modulation index around 0.85 (transformer ratios of 0.915 on the rectifier side and 1.015 on the inverter side). The converter reactor and the transformer leakage reactance permit the VSC output voltage to shift in phase and amplitude with respect to the AC system, and allows control of converter active and reactive power output.
To meet AC system harmonic specifications, AC filters form an essential part of the scheme. They can be connected as shunt elements on the AC system side or the converter side of the converter transformer. Since there are only high frequency harmonics, shunt filtering is therefore relatively small compared to the converter rating. It is sufficient with a high pass-filter and no tuned filters are needed. The later arrangement is used in our model and a converter reactor, an air cored device, separates the fundamental frequency (filter bus) from the raw PWM waveform (converter bus). The AC harmonics generation [4] mainly depends on the:
Type of modulation (e.g. single-phase or three-phase carrier based, space vector, etc.)
Frequency index p = carrier frequency / modulator frequency (e.g. p = 1350/50 = 27)
Modulation index m = fundamental output voltage of the converter / pole to pole DC voltage
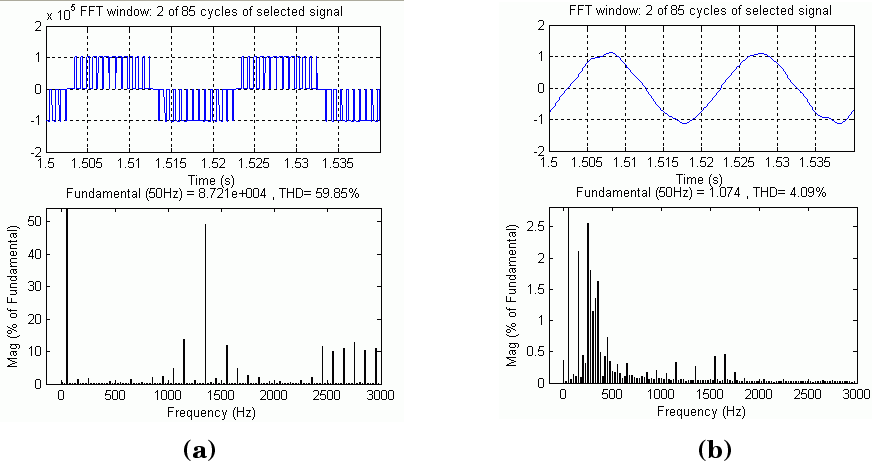
The principal harmonic voltages are generated at and around multiples of p. The shunt AC filters are 27th and 54th high pass totaling 40 Mvar. To illustrate the AC filter action, we did an FFT analysis in steady state of the converter phase A voltage and the filter bus phase A voltage, using the Powergui block. The results are shown in Phase A Voltage and FFT Analysis: (a) Converter Bus (b) Filter Bus.
Phase A Voltage and FFT Analysis: (a) Converter Bus (b) Filter Bus
The reservoir DC capacitors are connected to the VSC terminals. They have an influence on the system dynamics and the voltage ripple on the DC side. The size of the capacitor is defined by the time constant τ corresponding to the time it takes to charge the capacitor to the base voltage (100 kV) if it is charged with the base current (1 kA). This yields
τ = C · Zbase = 70e-6 · 100 = 7 ms
with Zbase = 100kV/1 kA
The DC side filters blocking high-frequency are tuned to the 3rd harmonic, i.e., the main harmonic present in the positive and negative pole voltages. It is shown that a reactive converter current generate a relatively large third harmonic in both the positive and negative pole voltages [3] but not in the total DC voltage. The DC harmonics can also be zero-sequence harmonics (odd multiples of 3) transferred to the DC side (e.g., through the grounded AC filters). A smoothing reactor is connected in series at each pole terminal.
To keep the DC side balanced, the level of the difference between the pole voltages has to be controlled and kept to zero (see the DC Voltage Balance Control block in the VSC Controller block).
The rectifier and the inverter are interconnected through a 75 km cable (2 pi sections). The use of underground cable is typical for VSC-HVDC links. A circuit breaker is used to apply a three-phase to ground fault on the inverter AC side. A Three-Phase Programmable Voltage Source block is used in station 1 system to apply voltage sags.
VSC Control System
Overview of the Control System of a VSC Converter and Interface to the Main Circuit shows an overview diagram of the VSC control system and its interface with the main circuit [3].
Overview of the Control System of a VSC Converter and Interface to the Main Circuit

The converter 1 and converter 2 controller designs are identical. The two controllers are independent with no communication between them. Each converter has two degrees of freedom. In our case, these are used to control:
P and Q in station 1 (rectifier)
Udc and Q in station 2 (inverter).
The control of the AC voltage would be also possible as an alternative to Q. This requires an extra regulator which is not implemented in our model.
Open the VSC Controller subsystem to see the details.
The sample time of the controller model (Ts_Control) is 74.06 µs, which is ten times the simulation sample time. The later is chosen to be one hundredth of the PWM carrier period (i.e., 0.01/1350 s) giving an acceptable simulation precision. The power elements, the anti-aliasing filters and the PWM Generator block use the fundamental sample time (Ts_Power) of 7.406 µs. The unsynchronized PWM mode of operation is chosen for our model.
The normalized sampled voltages and currents (in pu) are provided to the controller.
The Clark Transformations block transforms the three-phase quantities to space vector components α and β (real and imaginary part). The signal measurements (U and I) on the primary side are rotated by ±pi/6 according to the transformer connection (YD11 or YD1) to have the same reference frame with the signal measured on the secondary side of the transformer (see block CLARK YD).
The dq transformations block computes the direct axis “d” and the quadratic axis “q” quantities (two axis rotating reference frame) from the α and β quantities.
The Signal Calculations block calculates and filters quantities used by the controller (e.g., active and reactive power, modulation index, DC current and voltage, etc.).
Phase Locked Loop (PLL)
The Phase Locked Loop block measures the system frequency and provides the phase synchronous angle Θ (more precisely [sin(Θ), cos(Θ)]) for the dq Transformations block. In steady state, sin(Θ) is in phase with the fundamental (positive sequence) of the α component and phase A of the PCC voltage (Uabc).
Outer Active and Reactive Power and Voltage Loop
The active and reactive power and voltage loop contains the outer loop regulators that calculates the reference value of the converter current vector (Iref_dq) which is the input to the inner current loop. The control modes are: in the “d” axis, either the active power flow at the PCC or the pole-to-pole DC voltage; in the “q” axis, the reactive power flow at the PCC. Note that, it would be also possible to add an AC voltage control mode at the PCC in the “q” axis. The main functions of the Active and reactive power and voltage loop are described below.
The Reactive Power Control regulator block combines a PI control with a feedforward control to increase the speed response. To avoid integrator wind-up the following actions are taken: the error is reset to zero, when the measured PCC voltage is less than a constant value (i.e., during an AC perturbation); when the regulator output is limited, the limitation error is fed back with the right sign, to the integrator input. The AC Voltage control override block, based on two PI regulators, will override the reactive power regulator to maintain the PCC AC voltage within a secure range, especially in steady-state.
The Active Power Control block is similar to the Reactive Power Control block. The extra Ramping block ramps the power order towards the desired value with an adjusted rate when the control is de-blocked. The ramped value is reset to zero when the converter is blocked. The DC Voltage control override block, based on two PI regulators, will override the active power regulator to maintain the DC voltage within a secure range, especially during a perturbation in the AC system of the station controlling the DC voltage.
The DC Voltage Control regulator block uses a PI regulator. The block is enabled when the Active Power Control block is disabled. The block output is a reference value, for the “d” component of converter current vector, for the Current Reference Limitation block.
The Current Reference Calculation block transforms the active and reactive power references, calculated by the P and Q controllers, to current references according to the measured (space vector) voltage at the filter bus. The current reference is estimated by dividing the power reference by the voltage (up to a minimum preset voltage value).
The current reference vector is limited to a maximum acceptable value (i.e., equipment dependent) by the Current Reference Limitation block. In power control mode, equal scaling is applied to the active and reactive power reference when a limit is imposed. In DC voltage control mode, higher priority is given to the active power when a limit is imposed for an efficient control of the voltage.
Inner Current Loop
The main functions of Inner Current Loop block are described below.
The AC Current Control block tracks the current reference vector (“d” and “q” components) with a feed forward scheme to achieve a fast control of the current at load changes and disturbances (e.g., so short-circuit faults do not exceed the references) [3] [5] [6]. In essence, it consist of knowing the U_dq vector voltages and computing what the converter voltages have to be, by adding the voltage drops due to the currents across the impedance between the U and the PWM-VSC voltages. The state equations representing the dynamics of the VSC currents are used (an approximation is made by neglecting the AC filters). The “d” and “q” components are decoupled to obtain two independent first-order plant models. A proportional integral (PI) feedback of the converter current is used to reduce the error to zero in steady state. The output of the AC Current Control block is the unlimited reference voltage vector Vref_dq_tmp.
The Reference Voltage Conditioning block takes into account the actual DC voltage and the theoretical maximum peak value of the fundamental bridge phase voltage in relation to the DC voltage to generate the new optimized reference voltage vector. In our model (i.e., a three-level NPC with carrier based PWM), the ratio between the maximum fundamental peak phase voltage and the DC total voltage (i.e., for a modulation index of 1) is = 0.816. By choosing a nominal line voltage of 100 kV at the transformer secondary bus and a nominal total DC voltage of 200 kV the nominal modulation index would be 0.816. In theory, the converter should be able to generate up to 1/0.816 or 1.23 pu when the modulation index is equal to 1. This voltage margin is important for generating significant capacitive converter current (i.e., a reactive power flow to the AC system).
The Reference Voltage Limitation block limits the reference voltage vector amplitude to 1.0, since over modulation is not desired.
The Inverse dq and Inverse Clark transformation blocks are required to generate the three-phase voltage references to the PWM.
DC Voltage Balance Control
The DC Voltage Balance Control can be enabled or disabled. The difference between the DC side voltages (positive and negative) are controlled to keep the DC side of the three level bridge balanced (i.e., equal pole voltages) in steady-state. Small deviations between the pole voltages may occur at changes of active/reactive converter current or due to nonlinearity on lack of precision in the execution of the pulse width modulated bridge voltage. Furthermore, deviations between the pole voltages may be due to inherent unbalance in the circuit components impedance.
The DC midpoint current Id0 determines the difference Ud0 between the upper and lower DC voltages (DC Voltages and Currents of the Three-Level Bridge).
DC Voltages and Currents of the Three-Level Bridge

By changing the conduction time of the switches in a pole it is possible to change the average of the DC midpoint current Id0 and thereby control the difference voltage Ud0. For example, a positive difference (Ud0 ≥ 0) can be decreased to zero if the amplitude of the reference voltage which generates a positive midpoint current is increased at the same time as the amplitude of the reference voltage which generates a negative DC midpoint current is decreased. This is done by the addition of an offset component to the sinusoidal reference voltage. Consequently, the bridge voltage becomes distorted, and to limit the distortion effect, the control has to be slow. Finally, for better performance this function should be activated in the station controlling the DC voltage.
Dynamic Performance
In the next sections, the dynamic performance of the transmission system is verified by simulating and observing the
Dynamic response to step changes applied to the principal regulator references, like active/reactive power and DC voltage
Recovery from minor and severe perturbations in the AC system
For a comprehensive explanation of the procedure followed obtaining these results and more, refer to the Model Information block.
System Startup - Steady-State and Step Response
Startup and P & Q Step Responses in Station 1

Startup and Udc Step Response in Station 2

Station 2 converter controlling DC voltage is first deblocked at t=0.1 s. Then, station 1 controlling active power converter is deblocked at t=0.3 s and power is ramped up slowly to 1 pu. Steady state is reached at approximately t=1.3 s with DC voltage and power at 1.0 pu (200 kV, 200 MW). Both converters control the reactive power flow to a null value in station 1 and to 20 Mvar (-0.1 pu) into station 2 system.
After steady state has been reached, a -0.1 pu step is applied to the reference active power in converter 1 (t=1.5 s) and later a -0.1 pu step is applied to the reference reactive power (t=2.0 s). In station 2, a -0.05 pu step is applied to the DC voltage reference. The dynamic response of the regulators are observed. Stabilizing time is approximately 0.3 s.The control design attempts to decouple the active and reactive power responses. Note how the regulators are more or less mutually affected.
AC Side Perturbations
From the steady-state condition, a minor and a severe perturbation are executed at station 1 and 2 systems respectively. A three-phase voltage sag is first applied at station 1 bus. Then, following the system recovery, a three-phase to ground fault is applied at station 2 bus. The system recovery from the perturbations should be prompt and stable. The main waveforms from the scopes are reproduced in the two figures below.
Voltage Step on AC System 1

The AC voltage step (-0.1 pu) is applied at t=1.5 s during 0.14 s (7 cycles) at station 1. The results show that the active and reactive power deviation from the pre-disturbance is less than 0.09 pu and 0.2 pu respectively. The recovery time is less than 0.3 s and the steady state is reached before next perturbation initiation.
The fault is applied at t=2.1 s during 0.12 s (6 cycles) at station 2.
Three-Phase to Ground Fault at Station 2 Bus

Note that during the three-phase fault the transmitted DC power is almost halted and the DC voltage tends to increase (1.2 pu) since the DC side capacitance is being excessively charged. A special function (DC Voltage Control Override) in the Active Power Control (in station 1) attempts to limit the DC voltage within a fixed range. The system recovers well after the fault, within 0.5 s. Note the damped oscillations (around 10 Hz) in the reactive power.
References
[1] Weimers, L. “A New Technology for a Better Environment,” Power Engineering Review, IEEE®, vol. 18, issue 8, Aug. 1998.
[2] Schettler F., Huang H., and Christl N. “HVDC transmission systems using voltage source converters – design and applications,” IEEE Power Engineering Society Summer Meeting, July 2000.
[3] Lindberg, Anders “PWM and control of two and three level high power voltage source converters,” Licentiate thesis, ISSN-1100-1615, TRITA-EHE 9501, The Royal Institute of Technology, Sweden, 1995.
[4] Sadaba, Alonso, O., P. Sanchis Gurpide, J. Lopez Tanerna, I. Munoz Morales, L. Marroyo Palomo, “Voltage Harmonics Generated by 3-Level Converters Using PWM Natural Sampling,” Power Electronics Specialist Conference, 2001, IEEE 32nd Annual, 17–21 June 2001, vol. 3, pp. 1561–1565.
[5] Lu, Weixing, Boon-Teck Ooi, “Optimal Acquisition and Aggregation of Offshore wind Power by Multiterminal Voltage-Source HVDC,” IEEE Trans. Power Delivery, vol. 18, pp. 201–206, Jan. 2003.
[6] Sao, K., P.W. Lehn, M.R. Iravani, J.A. Martinez, “A benchmark system for digital time-domain simulation of a pulse-width-modulated D-STATCOM,” IEEE Trans. Power Delivery, vol. 17, pp. 1113–1120, Oct. 2002.
