Clarke Transform
Implement abc to αβ0 transform
Libraries:
Simscape /
Electrical /
Control /
Mathematical Transforms
Description
The Clarke Transform block converts the time-domain components of a three-phase system in an abc reference frame to components in a stationary ɑβ0 reference frame. The block can preserve the active and reactive powers with the powers of the system in the abc reference frame by implementing a power invariant version of the Clarke transform. For a balanced system, the zero component is equal to zero.
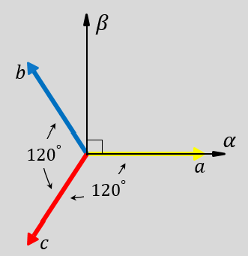
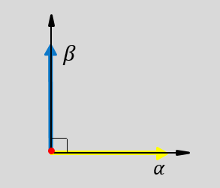
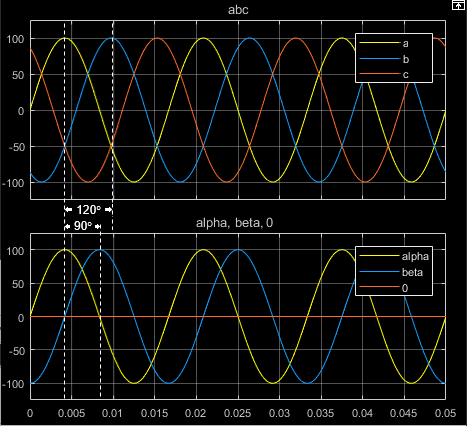
The figures show:
The direction of the magnetic axes of the stator windings in the abc reference frame and the stationary ɑβ0 reference frame
Equivalent ɑ, β, and zero components in the stationary reference frame
The time-response of the individual components of equivalent balanced abc and ɑβ0 systems
Equations
The block implements the Clarke transform as
where:
a, b, and c are the components of the three-phase system in the abc reference frame.
α and β are the components of the two-axis system in the stationary reference frame.
0 is the zero component of the two-axis system in the stationary reference frame.
The block implements the power invariant version of the Clarke transform as
Ports
Input
Output
Parameters
References
[1] Krause, P., O. Wasynczuk, S. D. Sudhoff, and S. Pekarek. Analysis of Electric Machinery and Drive Systems. Piscatawy, NJ: Wiley-IEEE Press, 2013.
Extended Capabilities
Version History
Introduced in R2017b