concentrationIndices
Compute ad-hoc concentration indices for a portfolio
Description
ci = concentrationIndices(PortfolioData)concentrationIndices function
supports the following indices:
CR — Concentration ratio
Deciles — Deciles of the portfolio weights distribution
Gini — Gini coefficient
HH — Herfindahl-Hirschman index
HK — Hannah-Kay index
HT — Hall-Tideman index
TE — Theil entropy index
[ adds
optional name-value pair arguments. ci,Lorenz]
= concentrationIndices(___,Name,Value)
Examples
Compute Concentration Indices for a Credit Portfolio
Compute the concentration indices for a credit portfolio using a portfolio that is described by its exposures. The exposures at default are stored in the EAD array.
Load the CreditPortfolioData.mat file that contains EAD used for the PortfolioData input argument.
load CreditPortfolioData.mat
ci = concentrationIndices(EAD)ci=1×8 table
ID CR Deciles Gini HH HK HT TE
___________ ________ _________________________________________________________________________________________________________________________ _______ ________ ________ ________ _______
"Portfolio" 0.058745 0 0.01118 0.026911 0.04605 0.072783 0.12318 0.18735 0.26993 0.41164 0.61058 1 0.55751 0.023919 0.013363 0.022599 0.53485
Compute Multiple Concentration Ratios
Use the CRIndex optional input to obtain the concentration ratios for the tenth and twentieth largest exposures. In the output, the CR column becomes a vector, with one value for each requested index.
Load the CreditPortfolioData.mat file that contains the EAD used for the PortfolioData input argument.
load CreditPortfolioData.mat ci = concentrationIndices(EAD,'CRIndex',[10 20])
ci=1×8 table
ID CR Deciles Gini HH HK HT TE
___________ __________________ _________________________________________________________________________________________________________________________ _______ ________ ________ ________ _______
"Portfolio" 0.38942 0.58836 0 0.01118 0.026911 0.04605 0.072783 0.12318 0.18735 0.26993 0.41164 0.61058 1 0.55751 0.023919 0.013363 0.022599 0.53485
Modify the Alpha Parameter of the Hannah-Kay Index
Use the HKAlpha optional input to set the alpha parameter for the Hannah-Kay (HK) index. Use a vector of alpha values to compute the HK index for multiple parameter values. In the output, the HK column becomes a vector, with one value for each requested alpha value.
Load the CreditPortfolioData.mat file that contains EAD used for the PortfolioData input argument.
load CreditPortfolioData.mat ci = concentrationIndices(EAD,'HKAlpha',[0.5 3])
ci=1×8 table
ID CR Deciles Gini HH HK HT TE
___________ ________ _________________________________________________________________________________________________________________________ _______ ________ ____________________ ________ _______
"Portfolio" 0.058745 0 0.01118 0.026911 0.04605 0.072783 0.12318 0.18735 0.26993 0.41164 0.61058 1 0.55751 0.023919 0.013363 0.029344 0.022599 0.53485
Create an ID to Compare Concentration Index Results
Compare the concentration measures using an ID optional argument for a fully diversified portfolio and a fully concentrated portfolio.
ciD = concentrationIndices([1 1 1 1 1],'ID','Fully diversified'); ciC = concentrationIndices([0 0 0 0 5],'ID','Fully concentrated'); disp([ciD;ciC])
ID CR Deciles Gini HH HK HT TE
____________________ ___ _______________________________________________________________________ ____ ___ ___ ___ ___________
"Fully diversified" 0.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.2 0.2 0.2 -2.2204e-16
"Fully concentrated" 1 0 0 0 0 0 0 0 0 0 0.5 1 0.8 1 1 1 1.6094
Apply Scaling to Concentration Indices
Use the ScaleIndices optional input to scale the index values of Gini, HH, HK, HT, and TE. The range of ScaleIndices is from 0 through 1, independent of the number of loans.
ciDU = concentrationIndices([1 1 1 1 1],'ID','Diversified, unscaled'); ciDS = concentrationIndices([1 1 1 1 1],'ID','Diversified, scaled','ScaleIndices',true); ciCU = concentrationIndices([0 0 0 0 5],'ID','Concentrated, unscaled'); ciCS = concentrationIndices([0 0 0 0 5],'ID','Concentrated, scaled','ScaleIndices',true); disp([ciDU;ciDS;ciCU;ciCS])
ID CR Deciles Gini HH HK HT TE
________________________ ___ _______________________________________________________________________ ____ __________ ___________ ___________ ___________
"Diversified, unscaled" 0.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.2 0.2 0.2 -2.2204e-16
"Diversified, scaled" 0.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 3.4694e-17 -3.4694e-17 -6.9389e-17 -1.3796e-16
"Concentrated, unscaled" 1 0 0 0 0 0 0 0 0 0 0.5 1 0.8 1 1 1 1.6094
"Concentrated, scaled" 1 0 0 0 0 0 0 0 0 0 0.5 1 1 1 1 1 1
Plot an Approximate Lorenz Curve Using Deciles Information
Load the CreditPortfolioData.mat file that contains EAD used for the PortfolioData input argument.
load CreditPortfolioData.mat
P = EAD;
ci = concentrationIndices(P);Visualize an approximate Lorenz curve using the deciles information and also the concentration at the decile level.
Proportion = 0:0.1:1; figure; subplot(2,1,1) area(Proportion',[ci.Deciles' Proportion'-ci.Deciles']) axis([0 1 0 1]) title('Lorenz Curve (By Deciles)') xlabel('Proportion of Loans') ylabel('Proportion of Value') subplot(2,1,2) bar(diff(ci.Deciles)) axis([0 11 0 1]) title('Concentration by Decile') xlabel('Decile') ylabel('Weight')

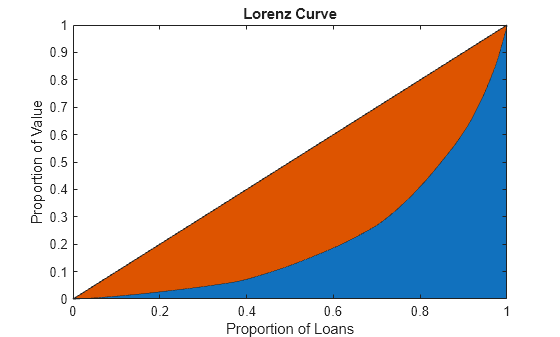
Plot an Exact Lorenz Curve Using the Optional Lorenz Output
Load the CreditPortfolioData.mat file that contains the EAD used for the PortfolioData input argument. The optional output Lorenz contains the data for the exact Lorenz curve.
load CreditPortfolioData.mat P = EAD; [~,Lorenz] = concentrationIndices(P); figure; area(Lorenz.ProportionLoans,[Lorenz.ProportionValue Lorenz.ProportionLoans-Lorenz.ProportionValue]) axis([0 1 0 1]) title('Lorenz Curve') xlabel('Proportion of Loans') ylabel('Proportion of Value')
Input Arguments
PortfolioData — Nonnegative portfolio positions in N assets
numeric array
Nonnegative portfolio positions in N assets,
specified as an N-by-1 (or 1-by-N)
numeric array.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: [ci,Lorenz] = concentrationIndices(PortfolioData,'CRIndex',100)
CRIndex — Index of interest for concentration ratio
1 (default) | nonnegative integer
Index of interest for the concentration ratio, specified as
the comma-separated pair consisting of 'CRIndex' and
an integer value between 1 and N,
where N is the number of assets in the portfolio.
The default value for CRIndex is 1 (the
default CR is the largest portfolio weight). If CRIndex is
a vector, the concentration ratio is computed for the index value
in the given order.
Data Types: double
HKAlpha — Alpha parameter for Hannah-Kay index
0.5 (default) | nonnegative numeric
Alpha parameter for Hannah-Kay index, specified as the comma-separated
pair consisting of 'HKAlpha', and a positive number
that cannot be equal to 1. If HKAlpha is
a vector, the Hannah-Kay index is computed for each alpha value in
the given order.
Data Types: double
ID — User-defined ID for portfolio
"Portfolio" (default) | character vector | string object
User-defined ID for the portfolio, specified as the comma-separated
pair consisting of 'ID' and a scalar string object
or character vector.
Data Types: char | string
ScaleIndices — Flag to indicate whether to scale concentration indices
false (no scaling) (default) | logical
Flag to indicate whether to scale concentration indices, specified
as the comma-separated pair consisting of 'ScaleIndices' and
a logical scalar. When the ScaleIndices is set
to true, the value of the Gini, HH, HK, HT,
and TE indices are scaled so that all these indices
have a minimum value of 0 (full diversification)
and a maximum value of 1 (full concentration).
Note
Scaling is applied only for portfolios with at least two assets. Otherwise, the scaling capability is undefined.
Data Types: logical
Output Arguments
ci — Concentration indices information for given portfolio
table
Concentration indices information for the given portfolio, returned as a table with the following columns:
ID— Portfolio ID string. Use theIDname-value pair argument to set it.CR— Concentration ratio. By default, the concentration ratio for the first index (largest portfolio weight) is reported. Use theCRIndexname-value pair argument to choose a different index. IfCRIndexis a vector of length m, thenCRis a row vector of size1-by-m. For more information, see More About.Deciles— Deciles of the portfolio weights distribution is a1-by-11row vector containing the values0, the nine decile cut points, and1. For more information, see More About.Gini— Gini coefficient. For more information, see More About.HH— Herfindahl-Hirschman index. For more information, see More About.HK— Hannah-Kay index (reciprocal). By default, the'alpha'parameter is set to0.5. Use theHKAlphaname-value pair argument to choose a different value. IfHKAlphais a vector of lengthm, thenHKis a row vector of size1-by-m. For more information, see More About.HT— Hall-Tideman index. For more information, see More About.TE— Theil entropy index. For more information, see More About.
Lorenz — Lorenz curve data
table
Lorenz curve data, returned as a table with the following columns:
ProportionLoans— (N+1)-by-1numeric array containing the values0,1/N,2/N, ...N/N=1. This is the data for the horizontal axis of the Lorenz curve.ProportionValue— (N+1)-by-1numeric array containing the proportion of portfolio value accumulated up to the corresponding proportion of loans in theProportionLoanscolumn. This is the data for the vertical axis of the Lorenz curve.
More About
Portfolio Notation
All the concentration indices for concentrationIndices assume
a credit portfolio with an exposure to counterparties.
Let P be a given credit portfolio with exposure
to N counterparties. Let x1,...xN represent
the exposures to each counterparty, with xi >
= 0 for all i = 1,...N.
And, let x be the total portfolio exposure
Assume that x > 0,
that is, at least one exposure is nonzero. The portfolio weights are
given by w1,...,wN with
The weights are sorted in non-decreasing order. The following standard notation uses brackets around the indices to denote ordered values.
Concentration Ratio
The concentration ratio (CR) answers the question “what proportion of the total exposure is accumulated in the largest k loans?”
The formula for the concentration ratio (CR) is:
For example, if k=1, CR1 is
a sum of the one term w[N-1+1] = w[N],
that is, it is the largest weight. For any k, the
CR index takes values from 0 through 1.
Lorenz Curve
The Lorenz curve is a visualization of the cumulative proportion of portfolio value (or cumulative portfolio weights) against the cumulative proportion of loans.
The cumulative proportion of loans (p) is defined by:
The cumulative proportion of portfolio value L is defined as:
The Lorenz curve is a plot of L versus p, or the cumulative proportion of portfolio value versus cumulative proportion of the number of loans (sorted from smallest to largest).
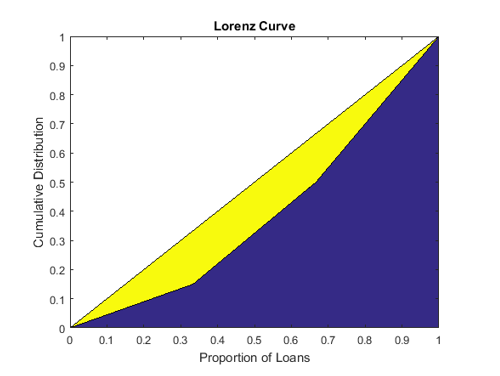
The diagonal line is indicated in the same plot because it represents the curve for the portfolio with the least possible concentration (all loans with the same weight). The area between the diagonal and the Lorenz curve is a visual representation of the Gini coefficient, which is another concentration measure.
Deciles
Deciles are commonly used in the context of income inequality.
If you sort individuals by their income level, what proportion
of the total income is earned by the lowest 10% and the lowest 20%
of the population? In a credit portfolio, loans can be sorted by exposure.
The first decile corresponds to the proportion of the portfolio value
that is accumulated by the smallest 10% loans, and so on. Deciles
are proportions, therefore they always take values from 0 through 1.
Defining the cumulative proportion of loans (p) and the cumulative proportion of values L as in Lorenz Curve, the deciles are a subset of the proportion of value array. Given indices d1, d2,..., d9 such that the proportion of loans matches exactly these values:
The deciles D0,D1,....,D9,D10 are defined as the corresponding proportion of values:
When the total number of loans N is not divisible by 10, no indices match the exact proportion of loans 0.1, 0.2, and so on. In that case, the decile values are linearly interpolated from the Lorenz curve data (that is, from the p and L arrays). With this definition, there are 11 values in the deciles information because the end points 0% and 100% are included.
Gini Index
The Gini index (or coefficient) is visualized on a Lorenz curve plot as the area between the diagonal and the Lorenz curve.
Technically, the Gini index is the ratio of that area to the area of the full triangle under the diagonal on the Lorenz curve plot. The Gini index is also defined equivalently as the average absolute difference between all the weights in the portfolio normalized by the average weight.
Using the proportion of values that array L defined in the Lorenz curve section, the Gini index is given by the formula:
Equivalently, the Gini index can be computed from the sorted weights directly with the formula:
The Gini coefficient values are always between 0 (full diversification) and
1 - 1/N (full
concentration).
Herfindahl-Hirschman Index
The Herfindahl-Hirschman index is commonly used as a measure of market concentration.
The formula for the Herfindahl-Hirschman index is:
The Herfindahl-Hirschman index takes values between 1/N (full
diversification) and 1 (full concentration).
Hannah-Kay Index
The Hannah-Kay index is a generalization of the Herfindahl-Hirschman index.
The formula for the Hannah-Kay depends on a parameter ɑ > 0, ɑ
≄ 1, as follows:
This formula is the reciprocal of the original Hannah-Kay index, which is defined with
1/(1 - ɑ) in the exponent. For
concentration analysis, the reciprocal formula is the standard because it increases
as the concentration increases. This is the formula implemented in
concentrationIndices. The Hannah-Kay index takes values
between 1/N (full diversification) and
1 (full concentration).
Hall-Tideman Index
The Hall-Tideman index is a measure commonly used for market concentration.
The formula for the Hall-Tideman index is:
The Hall-Tideman index takes values between 1/N (full
diversification) and 1 (full concentration).
Theil Entropy Index
The Theil entropy index, based on a traditional entropy measure (for example, Shannon entropy), is adjusted so that it increases as concentration increases (entropy moves in the opposite direction), and shifted to make it positive.
The formula for the Theil entropy index is:
The Theil entropy index takes values between 0 (full
diversification) and log(N)
(full concentration).
References
[1] Basel Committee on Banking Supervision. "Studies on Credit Risk Concentration". Working paper no. 15. November, 2006.
[2] Calabrese, R., and F. Porro. "Single-name concentration risk in credit portfolios: a comparison of concentration indices." working paper 201214, Geary Institute, University College, Dublin, May, 2012.
[3] Lütkebohmert, E. Concentration Risk in Credit Portfolios. Springer, 2009.
Version History
Introduced in R2017a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)