iconnect
(Not recommended) Create empty iconnect (interconnection)
objects
iconnect is not recommended. For model interconnections, use
connect instead.
Syntax
H = iconnect
Description
Interconnection objects (class iconnect) are an alternative to
sysic, and are used to build complex interconnections of uncertain
matrices and systems.
An iconnect object has 3 fields to be set by the user,
Input, Output and Equation.
Input and Output are icsignal
objects, while Equation.is a cell-array of equality constraints (using
equate) on icsignal objects. Once these are specified,
then the System property is the input/output model, implied by the
constraints in Equation. relating the variables defined in
Input and Output.
Examples
iconnect can be used to create the transfer matrix M
as described in the following figure.
![]()
Create three scalar icsignal:
r, e and y. Create an empty iconnect
object, M. Define the output of the interconnection to be [e;
y], and the input to be r. Define two constraints among the
variables: e = r-y, and y = (2/s) e. Get the transfer
function representation of the relationship between the input (r) and the
output [e; y].
r = icsignal(1);
e = icsignal(1);
y = icsignal(1);
M = iconnect;
M.Input = r;
M.Output = [e;y];
M.Equation{1} = equate(e,r-y);
M.Equation{2} = equate(y,tf(2,[1 0])*e);
tf(M.System)
The transfer functions from input to outputs are
s
#1: -----
s + 2
2
#2: -----
s + 2
By not explicitly introducing e, this can be done more concisely with
only one equality constraint.
r = icsignal(1);
y = icsignal(1);
N = iconnect;
N.Input = r;
N.Output = [r-y;y];
N.Equation{1} = equate(y,tf(2,[1 0])*(r-y));
tf(N.System)
You have created the same transfer functions from input to outputs.
s
#1: -----
s + 2
2
#2: -----
s + 2
You can also specify uncertain, multivariable interconnections using
iconnect. Consider two uncertain motor/generator constraints among 4
variables [V;I;T;W], V-R*I-K*W=0, and
T=K*I. Find the uncertain 2x2 matrix
B so that [V;T] = B*[W;I].
R = ureal('R',1,'Percentage',[-10 40]);
K = ureal('K',2e-3,'Percentage',[-30 30]);
V = icsignal(1);
I = icsignal(1);
T = icsignal(1);
W = icsignal(1);
M = iconnect;
M.Input = [W;I];
M.Output = [V;T];
M.Equation{1} = equate(V-R*I-K*W,iczero(1));
M.Equation{2} = equate(T,K*I);
B = M.System
UMAT: 2 Rows, 2 Columns
K: real, nominal = 0.002, variability = [-30 30]%, 2 occurrences
R: real, nominal = 1, variability = [-10 40]%, 1 occurrence
B.NominalValue
ans =
0.0020 1.0000
0 0.0020
A simple system interconnection, identical to the system illustrated in the sysic reference pages. Consider a three-input, two-output state-space matrix
T,
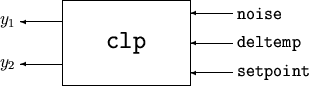
which has internal structure

P = rss(3,2,2);
K = rss(1,1,2);
A = rss(1,1,1);
W = rss(1,1,1);
M = iconnect;
noise = icsignal(1);
deltemp = icsignal(1);
setpoint = icsignal(1);
yp = icsignal(2);
rad2deg = 57.3
rad2deg =
57.3000
M.Equation{1} = equate(yp,P*[W*deltemp;A*K*[noise+yp(2);setpoint]]);
M.Input = [noise;deltemp;setpoint];
M.Output = [rad2deg*yp(1);setpoint-yp(2)];
T = M.System;
size(T)
State-space model with 2 outputs, 3 inputs, and 6 states.
Limitations
The syntax for iconnect objects and icsignals is
very flexible. Without care, you can build inefficient (i.e., nonminimal) representations
where the state dimension of the interconnection is greater than the sum of the state
dimensions of the components. This is in contrast to sysic. In
sysic, the syntax used to specify inputs to systems (the
input_to_ListedSubSystemName variable) forces you to include each
subsystem of the interconnection only once in the equations. Hence, interconnections formed
with sysic are componentwise minimal. That is, the state dimension of the
interconnection equals the sum of the state dimensions of the components.
Algorithms
Each equation represents an equality constraint among the variables. You choose the input
and output variables, and the imp2exp function makes the implicit
relationship between them explicit.
Version History
Introduced before R2006a
