aryule
Autoregressive all-pole model parameters — Yule-Walker method
Description
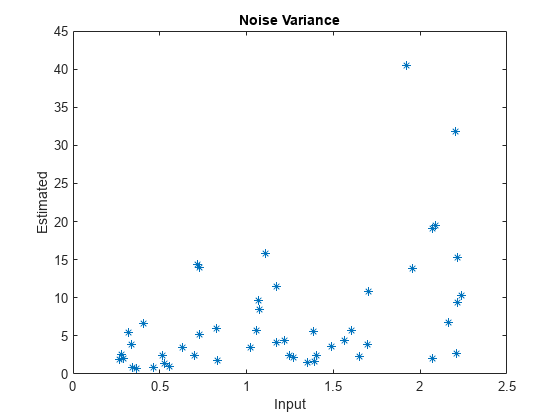
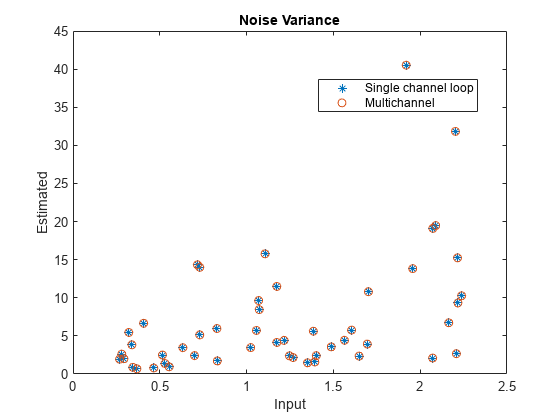
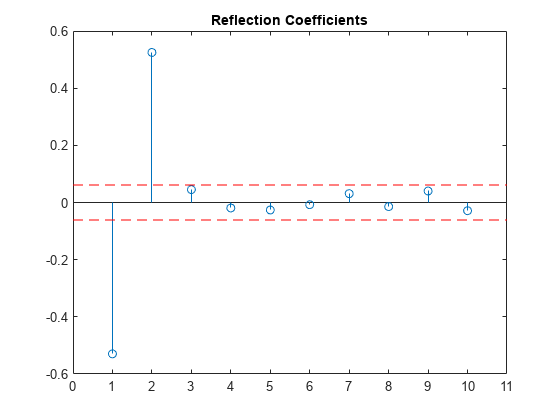
Examples
Input Arguments
Output Arguments
More About
Algorithms
aryule uses the Levinson-Durbin recursion on the biased estimate of the
sample autocorrelation sequence to compute the parameters.
References
[1] Hayes, Monson H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.
Extended Capabilities
Version History
Introduced before R2006a