modalfit
Modal parameters from frequency-response functions
Syntax
Description
fn = modalfit(frf,f,fs,mnum)mnum modes of a system with
measured frequency-response functions frf defined at frequencies
f and for a sample rate fs. Use
modalfrf to generate a matrix of
frequency-response functions from measured data. frf is assumed
to be in dynamic flexibility (receptance) format.
[___] = modalfit(
estimates the modal parameters of the identified model sys,f,mnum,Name,Value)sys. Use
estimation commands like ssest (System Identification Toolbox) or tfest (System Identification Toolbox) to create sys starting from a measured
frequency-response function or from time-domain input and output signals. This syntax
allows use of the 'DriveIndex',
'FreqRange', and 'PhysFreq' name-value
arguments. It typically requires less data than syntaxes that use nonparametric
methods. You must have a System Identification Toolbox™ license to use this syntax.
Examples
Frequency-Response Function of SISO System
Estimate the frequency-response function for a simple single-input/single-output system and compare it to the definition.
A one-dimensional discrete-time oscillating system consists of a unit mass, , attached to a wall by a spring with elastic constant . A sensor samples the displacement of the mass at Hz. A damper impedes the motion of the mass by exerting on it a force proportional to speed, with damping constant .

Generate 3000 time samples. Define the sampling interval .
Fs = 1; dt = 1/Fs; N = 3000; t = dt*(0:N-1); b = 0.01;
The system can be described by the state-space model
where is the state vector, and are respectively the displacement and velocity of the mass, is the driving force, and is the measured output. The state-space matrices are
is the identity, and the continuous-time state-space matrices are
Ac = [0 1;-1 -b]; A = expm(Ac*dt); Bc = [0;1]; B = Ac\(A-eye(2))*Bc; C = [1 0]; D = 0;
The mass is driven by random input for the first 2000 seconds and then left to return to rest. Use the state-space model to compute the time evolution of the system starting from an all-zero initial state. Plot the displacement of the mass as a function of time.
rng default u = randn(1,N)/2; u(2001:end) = 0; y = 0; x = [0;0]; for k = 1:N y(k) = C*x + D*u(k); x = A*x + B*u(k); end plot(t,y)

Estimate the modal frequency-response function of the system. Use a Hann window half as long as the measured signals. Specify that the output is the displacement of the mass.
wind = hann(N/2); [frf,f] = modalfrf(u',y',Fs,wind,'Sensor','dis');
The frequency-response function of a discrete-time system can be expressed as the Z-transform of the time-domain transfer function of the system, evaluated at the unit circle. Compare the modalfrf estimate with the definition.
[b,a] = ss2tf(A,B,C,D); nfs = 2048; fz = 0:1/nfs:1/2-1/nfs; z = exp(2j*pi*fz); ztf = polyval(b,z)./polyval(a,z); plot(f,20*log10(abs(frf))) hold on plot(fz*Fs,20*log10(abs(ztf))) hold off grid ylim([-60 40])

Estimate the natural frequency and the damping ratio for the vibration mode.
[fn,dr] = modalfit(frf,f,Fs,1,'FitMethod','PP')
fn = 0.1593
dr = 0.0043
Compare the natural frequency to , which is the theoretical value for the undamped system.
theo = 1/(2*pi)
theo = 0.1592
Modal Parameters Using Least-Squares Rational Function Method
Compute the modal parameters of a Space Station module starting from its frequency-response function (FRF) array.
Load a structure containing the three-input/three-output FRF array. The system is sampled at 320 Hz.
load modaldata SpaceStationFRF frf = SpaceStationFRF.FRF; f = SpaceStationFRF.f; fs = SpaceStationFRF.Fs;
Extract the modal parameters of the lowest 24 modes using the least-squares rational function method.
[fn,dr,ms,ofrf] = modalfit(frf,f,fs,24,'FitMethod','lsrf');
Compare the reconstructed FRF array to the measured one.
for ij = 1:3 for ji = 1:3 subplot(3,3,3*(ij-1)+ji) loglog(f,abs(frf(:,ji,ij))) hold on loglog(f,abs(ofrf(:,ji,ij))) hold off axis tight title(sprintf('In%d -> Out%d',ij,ji)) if ij==3 xlabel('Frequency (Hz)') end end end

Modal Analysis of Two-Body Oscillator
Estimate the modal parameters of a multi-input/multi-output (MIMO) system.
Two masses connected to a spring and a damper on each side form an ideal one-dimensional discrete-time oscillating system. The system input array u consists of random driving forces applied to the masses. The system output array y contains the observed displacements of the masses from their initial reference positions. The system is sampled at a rate Fs of 40 Hz.

Load the data file containing the MIMO system inputs, the system outputs, and the sample rate. The example Frequency-Response Analysis of MIMO System analyzes the system that generated the data used in this example.
load MIMOdataEstimate the modal frequency response functions of the system. Use a 12000-sample Hann window with 9000 samples of overlap between adjoining segments. Specify the sensor data type as measured displacements.
wind = hann(12000);
nove = 9000;
[frf,f] = modalfrf(u,y,Fs,wind,nove,Sensor="dis");Estimate the natural frequencies, damping ratios, and mode shapes of the system. Use two modes and pick the least-squares rational function estimation method for the calculation.
[fn,dr,ms] = modalfit(frf,f,Fs,2,FitMethod="lsrf")fn = 2×1
3.8477
14.4259
dr = 2×1
0.0030
0.0113
ms = 2×2 complex
0.0819 - 0.1139i 0.0016 - 0.0109i
0.0442 - 0.0615i -0.0602 + 0.2041i
Modal Parameters of MIMO System
Compute the natural frequencies, the damping ratios, and the mode shapes for a two-input/three-output system excited by several bursts of random noise. Each burst lasts for 1 second, and there are 2 seconds between the end of each burst and the start of the next. The data are sampled at 4 kHz.
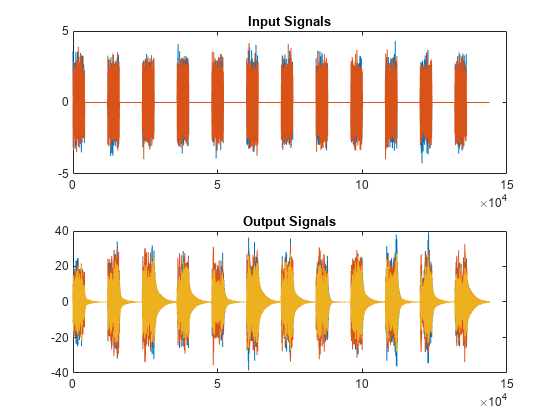
Load the data file. Plot the input signals and the output signals.
load modaldata subplot(2,1,1) plot(Xburst) title('Input Signals') subplot(2,1,2) plot(Yburst) title('Output Signals')
Compute the frequency-response functions. Specify a rectangular window with length equal to the burst period and no overlap between adjoining segments.
burstLen = 12000; [frf,f] = modalfrf(Xburst,Yburst,fs,burstLen);
Visualize a stabilization diagram and return the stable natural frequencies. Specify a maximum model order of 30 modes.
figure
modalsd(frf,f,fs,'MaxModes',30);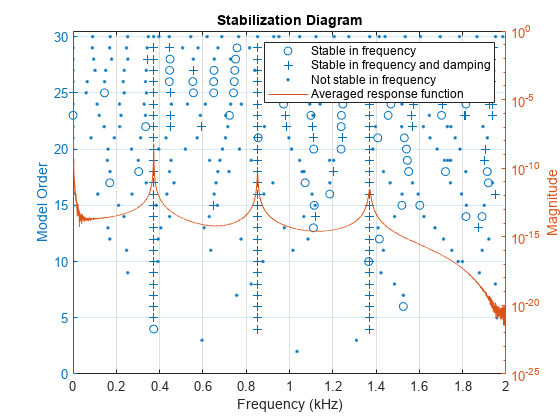
Zoom in on the plot. The averaged response function has maxima at 373 Hz, 852 Hz, and 1371 Hz, which correspond to the physical frequencies of the system. Save the maxima to a variable.
phfr = [373 852 1371];
Compute the modal parameters using the least-squares complex exponential (LSCE) algorithm. Specify a model order of 6 modes and specify physical frequencies for the 3 modes determined from the stabilization diagram. The function generates one set of natural frequencies and damping ratios for each input reference.
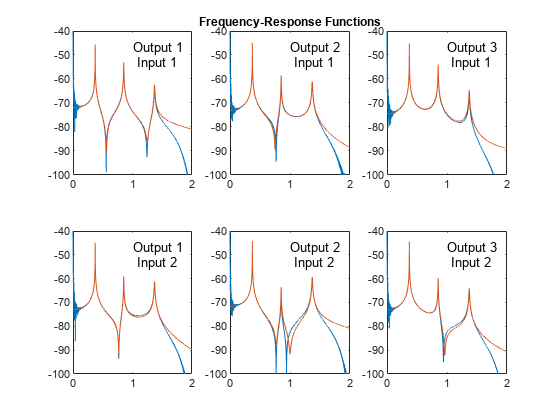
[fn,dr,ms,ofrf] = modalfit(frf,f,fs,6,'PhysFreq',phfr);Plot the reconstructed frequency-response functions and compare them to the original ones.
for k = 1:2 for m = 1:3 subplot(2,3,m+3*(k-1)) plot(f/1000,10*log10(abs(frf(:,m,k)))) hold on plot(f/1000,10*log10(abs(ofrf(:,m,k)))) hold off text(1,-50,[['Output ';' Input '] num2str([m k]')]) ylim([-100 -40]) end end subplot(2,3,2) title('Frequency-Response Functions')
Input Arguments
frf — Frequency-response functions
vector | matrix | 3-D array
Frequency-response functions, specified as a vector, matrix, or 3-D array.
frf has size
p-by-m-by-n, where
p is the number of frequency bins, m is
the number of response signals, and n is the number of
excitation signals used to estimate the transfer function.
frf is assumed to be in dynamic flexibility (receptance)
format.
Use modalfrf to generate a matrix of
frequency-response functions from measured data.
Example: Undamped Harmonic Oscillator
The motion of a simple undamped harmonic oscillator of unit mass and elastic constant sampled at a rate is described by the transfer function
,
where the numerator depends on the magnitude being measured:
Displacement:
Velocity:
Acceleration:
Compute the frequency-response function for the three possible system response sensor types. Use a sample rate of 2 Hz and 30,000 samples of white noise as input.
fs = 2; dt = 1/fs; N = 30000; u = randn(N,1); ydis = filter((1-cos(dt))*[0 1 1],[1 -2*cos(dt) 1],u); [frfd,fd] = modalfrf(u,ydis,fs,hann(N/2),Sensor="dis"); yvel = filter(sin(dt)*[0 1 -1],[1 -2*cos(dt) 1],u); [frfv,fv] = modalfrf(u,yvel,fs,hann(N/2),Sensor="vel"); yacc = filter([1 -(1+cos(dt)) cos(dt)],[1 -2*cos(dt) 1],u); [frfa,fa] = modalfrf(u,yacc,fs,hann(N/2),Sensor="acc"); loglog(fd,abs(frfd),fv,abs(frfv),fa,abs(frfa)) grid legend(["dis" "vel" "acc"],Location="best")

In all cases, the generated frequency-response function is in a format corresponding to displacement. Velocity and acceleration measurements are first and second time derivatives, respectively, of displacement measurements. The frequency-response functions are equivalent in the range around the natural frequency of the system. Away from the natural frequency, the frequency-response functions differ.
Data Types: single | double
Complex Number Support: Yes
f — Frequencies
vector
Frequencies, specified as a vector. The number of elements of f must
equal the number of rows of frf.
Data Types: single | double
fs — Sample rate of measurement data
positive scalar
Sample rate of measurement data, specified as a positive scalar expressed in hertz.
Data Types: single | double
mnum — Number of modes
positive integer
Number of modes, specified as a positive integer.
Data Types: single | double
sys — Identified system
model with identified parameters
Identified system, specified as a model with identified parameters. Use
estimation commands like ssest (System Identification Toolbox), n4sid (System Identification Toolbox), or tfest (System Identification Toolbox) to create
sys starting from a measured frequency-response function
or from time-domain input and output signals. See Modal Analysis of Identified Models for an
example. You must have a System Identification Toolbox license to use this input argument.
Example: idss([0.5418 0.8373;-0.8373 0.5334],[0.4852;0.8373],[1
0],0,[0;0],[0;0],1) generates an identified state-space model
corresponding to a unit mass attached to a wall by a spring of unit elastic
constant and a damper with constant 0.01. The displacement of the mass is sampled
at 1 Hz.
Example: idtf([0 0.4582 0.4566],[1 -1.0752 0.99],1) generates
an identified transfer-function model corresponding to a unit mass attached to a
wall by a spring of unit elastic constant and a damper with constant 0.01. The
displacement of the mass is sampled at 1 Hz.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'FitMethod','pp','FreqRange',[0 500] uses
the peak-picking method to perform the fit and restricts the frequency
range to between 0 and 500 Hz.
Feedthrough — Presence of feedthrough in estimated transfer function
false (default) | true
Presence of feedthrough in estimated transfer function, specified as a
logical value. This argument is available only if
'FitMethod' is specified as
'lsrf'.
Data Types: logical
FitMethod — Fitting algorithm
'lsce' (default) | 'lsrf' | 'pp'
Fitting algorithm, specified as 'lsce', 'lsrf', or
'pp'.
'lsce'— Least-Squares Complex Exponential Method. If you specify'lsce', thenfnis a vector withmnumelements, independent of the size offrf.'lsrf'— Least-squares rational function estimation method. If you specify'lsrf', thenfnis a vector withmnumelements, independent of the size offrf. The method is described in [3]. See Continuous-Time Transfer Function Estimation Using Continuous-Time Frequency-Domain Data (System Identification Toolbox) for more information. This algorithm typically requires less data than nonparametric approaches and is the only one that works for nonuniformf.'pp'— Peak-Picking Method. For anfrfcomputed from n excitation signals and m response signals,fnis anmnum-by-m-by-n array with one estimate offnand one estimate ofdrperfrf.
FreqRange — Frequency range
two-element vector of increasing positive values
Frequency range, specified as a two-element vector of increasing positive
values contained within the range specified in f.
Data Types: single | double
PhysFreq — Natural frequencies for physical modes
vector
Natural frequencies for physical modes to include in the analysis, specified as a vector of
frequency values within the range spanned by f. The
function includes in the analysis those modes with natural frequencies closest
to the values specified in the vector. If the vector contains
m frequency values, then fn and
dr have m rows each, and
ms has m columns. If you do not
specify this argument, then the function uses the entire frequency range in
f.
Data Types: single | double
DriveIndex — Indices of the driving-point frequency-response function
[1 1] (default) | two-element vector of positive integers
Indices of the driving-point frequency-response function, specified as a two-element vector of positive integers. The first element of the vector must be less than or equal to the number of system responses. The second element of the vector must be less than or equal to the number of system excitations. Mode shapes are normalized to unity modal based on the driving point.
Example: 'DriveIndex',[2 3] specifies that
the driving-point frequency-response function is frf(:,2,3).
Data Types: single | double
Output Arguments
fn — Natural frequencies
matrix | 3-D array
Natural frequencies, returned as a matrix or 3-D array. The size of fn
depends on the choice of fitting algorithm specified with
'FitMethod':
If you specify
'lsce'or'lsrf', thenfnis a vector withmnumelements, independent of the size offrf. If the system has more thanmnumoscillatory modes, then the'lsrf'method returns the firstmnumleast-damped modes sorted in order of increasing natural frequency.If you specify
'pp', thenfnis an array of sizemnum-by-m-by-n with one estimate offnand one estimate ofdrperfrf.
dr — Damping ratios
matrix | 3-D array
Damping ratios for the natural frequencies in fn,
returned as a matrix or 3-D array of the same size as fn.
ms — Mode-shape vectors
matrix
Mode-shape vectors, returned as a matrix. ms has mnum columns,
each containing a mode-shape vector of length q,
where q is the larger of the number of excitation
channels and the number of response channels.
ofrf — Reconstructed frequency-response functions
vector | matrix | 3-D array
Reconstructed frequency-response functions, returned as a vector,
matrix, or 3-D array with the same size as frf.
Algorithms
Least-Squares Complex Exponential Method
The least-squares complex exponential method computes the impulse response corresponding to each frequency-response function and fits to the response a set of complex damped sinusoids using Prony’s method.
A sampled damped sinusoid can be cast in the form
where:
fs is the sample rate.
fi is the sinusoid frequency.
bi is the damping coefficient.
Ai and ϕi are the amplitude and phase of the sinusoid.
The ai are called amplitudes and the xi are called poles. Prony’s method expresses a sampled function h(n) as a superposition of N/2 modes (and thus N amplitudes and poles):
The poles are the roots of a polynomial with coefficients c0, c1, …, cN–1:
The coefficients are found using an autoregressive model of L = 2N samples of h:
To find the poles, the algorithm uses the roots function. Once the poles are known, it is possible to determine the
frequencies and damping factors by identifying the imaginary and real parts of the pole
logarithms. The final step is solving for the amplitudes and reconstructing the impulse
response using
The following naive MATLAB® implementation summarizes the procedure:
N = 4; L = 2*N; h = rand(L,1); c = hankel(h(1:N),h(L-N:L-1))\-h(N+1:L); x = roots([1;c(N:-1:1)]).'; p = log(x); hrec = x.^((0:L-1)')*(x.^((0:L-1)')\h(1:L)); sum(h-hrec)
ans = 3.2613e-15 - 1.9297e-16i
Peak-Picking Method
The peak-picking method assumes that each significant peak in the frequency-response function corresponds to exactly one natural mode. Close to a peak, the system is assumed to behave like a one-degree-of-freedom damped harmonic oscillator:
where H is the frequency-response function, fr is the undamped resonance frequency, ζr = b/(4mk)1/2 is the relative damping, b is the damping constant, k is the elastic constant, and m is the mass.
Given a peak located at fp, the procedure takes the peak and a fixed number of points to either side, replaces the mass term with a dummy variable, d, and computes the modal parameters by solving the system of equations
References
[1] Allemang, Randall J., and David L. Brown. “Experimental Modal Analysis and Dynamic Component Synthesis, Vol. III: Modal Parameter Estimation.” Technical Report AFWAL-TR-87-3069. Air Force Wright Aeronautical Laboratories, Wright-Patterson Air Force Base, OH, December 1987.
[2] Brandt, Anders. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. Chichester, UK: John Wiley & Sons, 2011.
[3] Ozdemir, Ahmet Arda, and Suat Gumussoy. "Transfer Function Estimation in System Identification Toolbox via Vector Fitting." Proceedings of the 20th World Congress of the International Federation of Automatic Control, Toulouse, France, July 2017.
Version History
Introduced in R2017a
See Also
modalfrf | modalsd | n4sid (System Identification Toolbox) | tfest (System Identification Toolbox) | tfestimate
Topics
- Modal Analysis of Identified Models
- System Identification Overview (System Identification Toolbox)
- System Identification Workflow (System Identification Toolbox)
- Supported Continuous- and Discrete-Time Models (System Identification Toolbox)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)