sigwin.gausswin Class
Namespace: sigwin
Construct Gaussian window object
Description
Note
The use of sigwin.gausswin is not recommended.
Use gausswin instead.
sigwin.gausswin creates a handle to a Gaussian
window object for use in spectral analysis and FIR filtering by the
window method. Object methods enable workspace import and ASCII file
export of the window values.
The following equation defines the Gaussian window of length N:
where M=(N-1)/2 and x is
a linearly spaced vector of length N.
Equating with the usual standard deviation of a Gaussian value, , note:
Construction
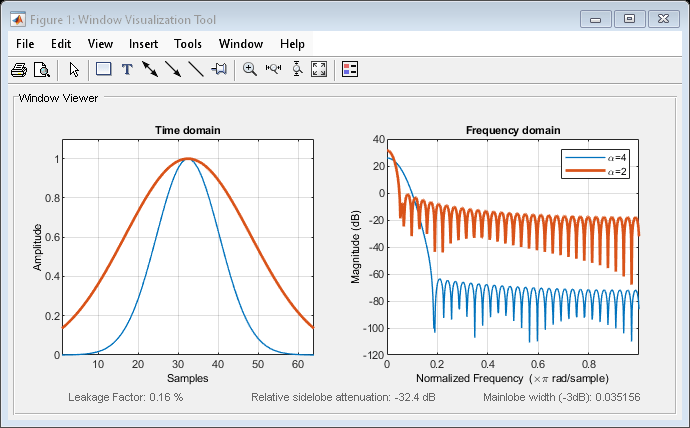
H = sigwin.gausswin returns a Gaussian
window object H of length 64 and dispersion parameter alpha of
2.5.
H = sigwin.gausswin( returns
a Gaussian window object Length)H of length Length and
dispersion parameter alpha of 2.5. Length requires
a positive integer. Entering a positive noninteger value for Length rounds
the length to the nearest integer. Entering a 1 for Length results
in a window with a single value of 1.
H = sigwin.gausswin( returns
a Gaussian window object with dispersion parameter Length,Alpha)alpha. alpha requires
a nonnegative real number and is inversely proportional to the standard
deviation of a Gaussian value.
Properties
|
Gaussian window length. The window length requires a positive
integer. Entering a positive noninteger value for |
|
Width of Gaussian window. |
Methods
| generate | Generates Gaussian window |
| info | Display information about Gaussian window object |
| winwrite | Save Gaussian window in ASCII file |
Copy Semantics
Handle. To learn how copy semantics affect your use of the class, see Copying Objects in the MATLAB® Programming Fundamentals documentation.
Examples
References
harris, fredric j. “On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform.” Proceedings of the IEEE®. Vol. 66, January 1978, pp. 51–83.