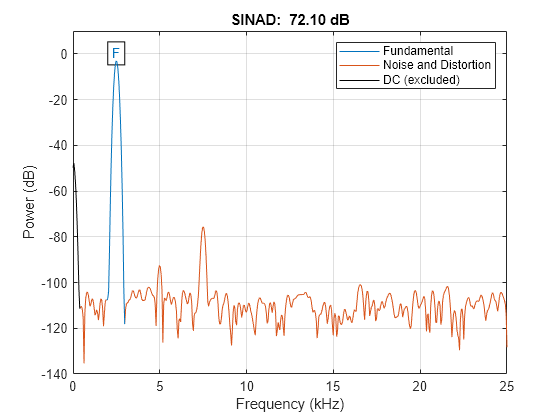
The functions thd, sfdr, sinad,
and snr measure the response
of a weakly nonlinear system stimulated by a sinusoid.
When given time-domain input, sinad performs
a periodogram using a Kaiser window with large sidelobe attenuation.
To find the fundamental frequency, the algorithm searches the periodogram
for the largest nonzero spectral component. It then computes the central
moment of all adjacent bins that decrease monotonically away from
the maximum. To be detectable, the fundamental should be at least
in the second frequency bin. Higher harmonics are at integer multiples
of the fundamental frequency. If a harmonic lies within the monotonically
decreasing region in the neighborhood of another, its power is considered
to belong to the larger harmonic. This larger harmonic may or may
not be the fundamental.
The function estimates a noise level using the median power
in the regions containing only noise and distortion. The DC component
is excluded from the calculation. The noise at each point is the estimated
level or the ordinate of the point, whichever is smaller. The noise
is then subtracted from the values of the signal and the harmonics.
sinad fails if the fundamental
is not the highest spectral component in the signal.
Ensure that the frequency components are far enough apart to accommodate for the sidelobe
width of the Kaiser window. If this is not feasible, you can use the
"power" flag and compute a periodogram with a different
window.