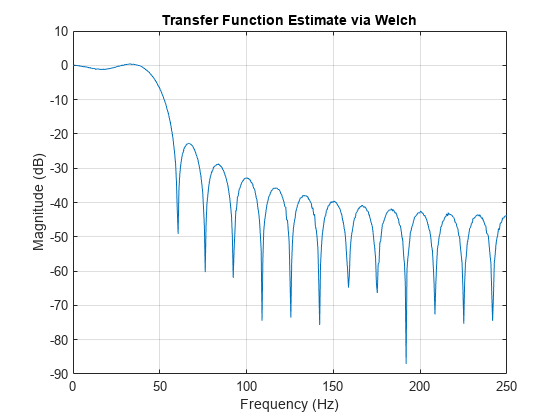
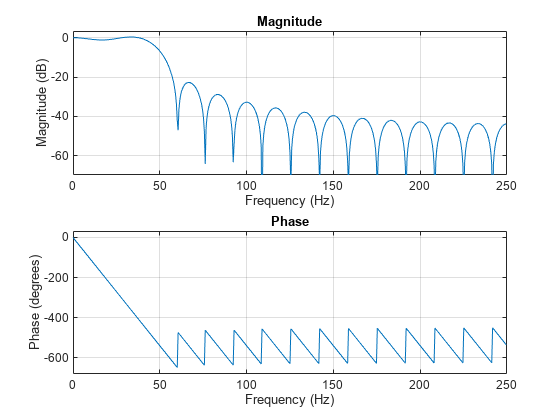
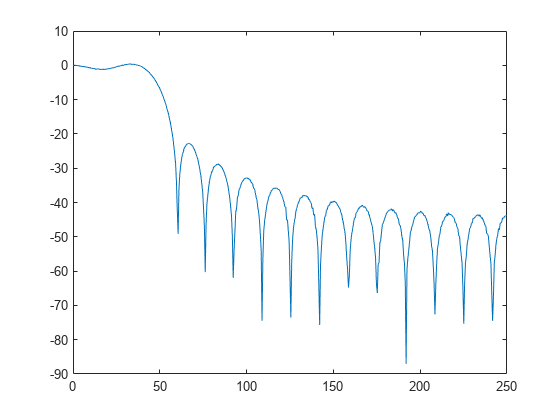
tfestimate
Transfer function estimate
Syntax
Description
txy = tfestimate(x,y)x and the output signal y
evaluated at a set of frequencies.
If
xandyare both vectors, they must have the same length.If one of the signals is a matrix and the other is a vector, then the length of the vector must equal the number of rows in the matrix. The function expands the vector and returns a matrix of column-by-column transfer function estimates.
If
xandyare matrices with the same number of rows but different numbers of columns, thentxyis a multi-input/multi-output (MIMO) transfer function that combines all input and output signals.txyis a three-dimensional array. Ifxhas m columns andyhas n columns, thentxyhas n columns and m pages. See Transfer Function for more information.If
xandyare matrices of equal size, thentfestimateoperates column-wise:txy(:,n) = tfestimate(x(:,n),y(:,n)). To obtain a MIMO estimate, append'mimo'to the argument list.
txy = tfestimate(___,'mimo')
[
returns a vector of frequencies, txy,f] = tfestimate(___,fs)f, expressed in terms of
the sample rate, fs, at which the transfer function is
estimated. fs must be the sixth numeric input to
tfestimate. To input a sample rate and still use the
default values of the preceding optional arguments, specify these arguments as
empty [].
[___] = tfestimate(___,'Estimator',
estimates transfer functions using the estimator est)est. Valid
options for est are 'H1' and
'H2'.
tfestimate(___) with
no output arguments plots the transfer function estimate in the current
figure window.
Examples
Input Arguments
Output Arguments
More About
Algorithms
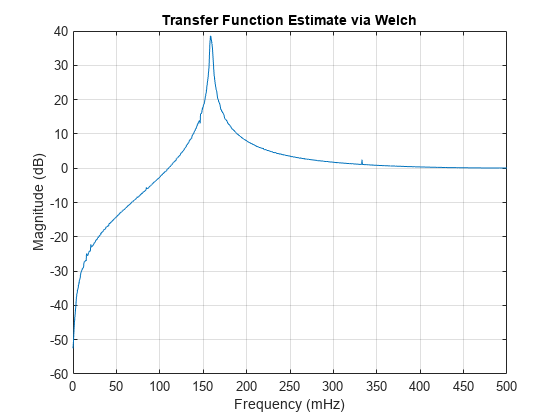
tfestimate uses Welch's averaged periodogram
method. See pwelch for details.
References
[1] Vold, Håvard, John Crowley, and G. Thomas Rocklin. “New Ways of Estimating Frequency Response Functions.” Sound and Vibration. Vol. 18, November 1984, pp. 34–38.
Extended Capabilities
Version History
Introduced before R2006aSee Also
cpsd | mscohere | periodogram | pwelch