Cross-Correlation of Two Moving Average Processes
This example shows how to find and plot the cross-correlation sequence between two moving average processes. The example compares the sample cross-correlation with the theoretical cross-correlation. Filter an white noise input with two different moving average filters. Plot the sample and theoretical cross-correlation sequences.
Create an white noise sequence. Set the random number generator to the default settings for reproducible results. Create two moving average filters. One filter has impulse response . The other filter has impulse response .
rng default
w = randn(100,1);
x = filter([1 1],1,w);
y = filter([1 -1],1,w);Obtain the sample cross-correlation sequence up to lag 20. Plot the sample cross-correlation along with the theoretical cross-correlation.
[xc,lags] = xcorr(x,y,20,'biased'); Xc = zeros(size(xc)); Xc(20) = -1; Xc(22) = 1; stem(lags,xc,'filled') hold on stem(lags,Xc,'.','linewidth',2) q = legend('Sample cross-correlation','Theoretical cross-correlation'); q.Location = 'NorthWest'; q.FontSize = 9; q.Box = 'off';
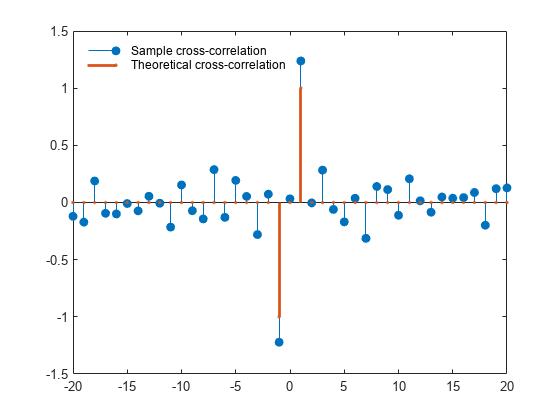
The theoretical cross-correlation is at lag , at lag , and zero at all other lags. The sample cross-correlation sequence approximates the theoretical cross-correlation.
As expected, there is not perfect agreement between the theoretical cross-correlation and sample cross-correlation. The sample cross-correlation does accurately represent both the sign and magnitude of the theoretical cross-correlation sequence values at lag and lag .
