Compute and Display Order-RPM Map
Generate a signal that consists of two linear chirps and a quadratic chirp, all sampled at 600 Hz for 5 seconds. The system that produces the signal increases its rotational speed from 10 to 40 revolutions per second during the testing period.
Generate the tachometer readings.
fs = 600; t1 = 5; t = 0:1/fs:t1; f0 = 10; f1 = 40; rpm = 60*linspace(f0,f1,length(t));
The linear chirps have orders 1 and 2.5. The component with order 1 has twice the amplitude of the other. The quadratic chirp starts at order 6 and returns to this order at the end of the measurement. Its amplitude is 0.8. Create the signal using this information.
o1 = 1; o2 = 2.5; o6 = 6; x = 2*chirp(t,o1*f0,t1,o1*f1)+chirp(t,o2*f0,t1,o2*f1) + ... 0.8*chirp(t,o6*f0,t1,o6*f1,'quadratic');
Compute the order-RPM map of the signal. Use the peak amplitude at each measurement cell. Specify a resolution of 0.25 orders. Window the data with a Chebyshev window whose sidelobe attenuation is 50 dB.
[map,or,rp] = rpmordermap(x,fs,rpm,0.25, ... 'Amplitude','peak','Window',{'chebwin',50});
Draw the order-RPM map as a waterfall plot.
[OR,RP] = meshgrid(or,rp); waterfall(OR,RP,map') view(-15,45) xlabel('Order') ylabel('RPM') zlabel('Amplitude')

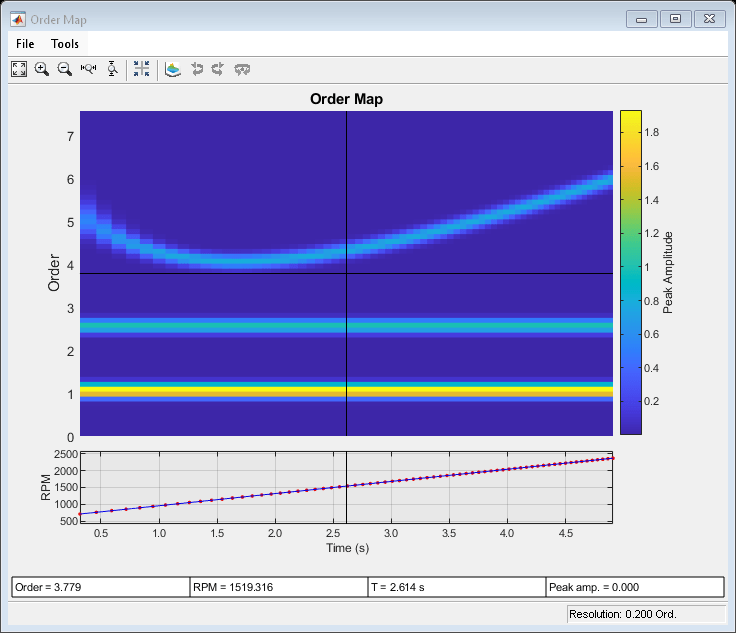
Use rpmordermap with no output arguments to display the map. Specify a resolution of 0.2 orders and 80% overlap between adjoining segments. Set the sidelobe attenuation of the Chebyshev window to 80 dB.
rpmordermap(x,fs,rpm,0.2, ... 'Amplitude','peak','OverlapPercent',80,'Window',{'chebwin',80})
See Also
orderspectrum | ordertrack | orderwaveform | rpmfreqmap | rpmordermap | tachorpm
