Downsampling — Signal Phases
This example shows how to use downsample to obtain the phases of a signal. Downsampling a signal by M can produce M unique phases. For example, if you have a discrete-time signal, x, with x(0) x(1) x(2) x(3), ..., the M phases of x are x(nM + k) with k = 0,1, ..., M-1.
The M signals are referred to as the polyphase components of x.
Create a white noise vector and obtain the 3 polyphase components associated with downsampling by 3.
Reset the random number generator to the default settings to produce a repeatable result. Generate a white noise random vector and obtain the 3 polyphase components associated with downsampling by 3.
rng default
x = randn(36,1);
x0 = downsample(x,3,0);
x1 = downsample(x,3,1);
x2 = downsample(x,3,2);
The polyphase components have length equal to 1/3 the original signal.
Upsample the polyphase components by 3 using upsample.
y0 = upsample(x0,3,0); y1 = upsample(x1,3,1); y2 = upsample(x2,3,2);
Plot the result.
subplot(4,1,1) stem(x,'Marker','none') title('Original Signal') ylim([-4 4]) subplot(4,1,2) stem(y0,'Marker','none') ylabel('Phase 0') ylim([-4 4]) subplot(4,1,3) stem(y1,'Marker','none') ylabel('Phase 1') ylim([-4 4]) subplot(4,1,4) stem(y2,'Marker','none') ylabel('Phase 2') ylim([-4 4])
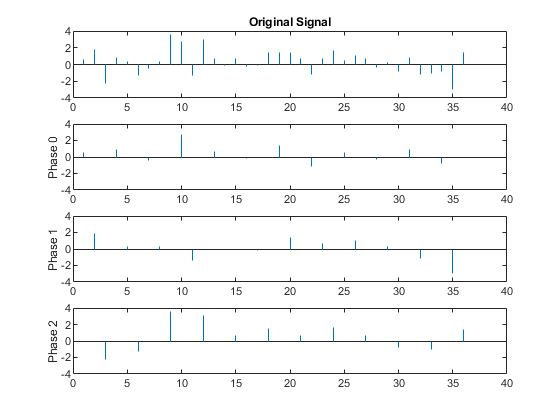
If you sum the upsampled polyphase components you obtain the original signal.
Create a discrete-time sinusoid and obtain the 2 polyphase components associated with downsampling by 2.
Create a discrete-time sine wave with an angular frequency of 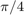 rad/sample. Add a DC offset of 2 to the sine wave to help with visualization of the polyphase components. Downsample the sine wave by 2 to obtain the even and odd polyphase components.
rad/sample. Add a DC offset of 2 to the sine wave to help with visualization of the polyphase components. Downsample the sine wave by 2 to obtain the even and odd polyphase components.
n = 0:127; x = 2+cos(pi/4*n); x0 = downsample(x,2,0); x1 = downsample(x,2,1);
Upsample the two polyphase components.
y0 = upsample(x0,2,0); y1 = upsample(x1,2,1);
Plot the upsampled polyphase components along with the original signal for comparison.
subplot(3,1,1) stem(x,'Marker','none') ylim([0.5 3.5]) title('Original Signal') subplot(3,1,2) stem(y0,'Marker','none') ylim([0.5 3.5]) ylabel('Phase 0') subplot(3,1,3) stem(y1,'Marker','none') ylim([0.5 3.5]) ylabel('Phase 1')
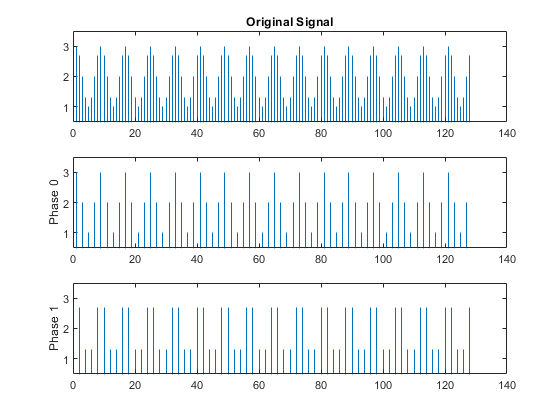
If you sum the two upsampled polyphase components (Phase 0 and Phase 1), you obtain the original sine wave.
