Modal Parameters of MIMO System
Compute the natural frequencies, the damping ratios, and the mode shapes for a two-input/three-output system excited by several bursts of random noise. Each burst lasts for 1 second, and there are 2 seconds between the end of each burst and the start of the next. The data are sampled at 4 kHz.
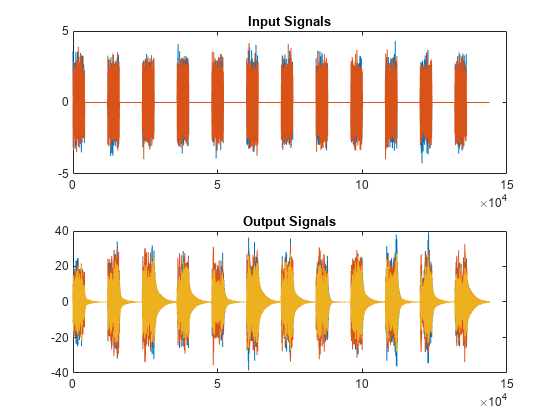
Load the data file. Plot the input signals and the output signals.
load modaldata subplot(2,1,1) plot(Xburst) title('Input Signals') subplot(2,1,2) plot(Yburst) title('Output Signals')
Compute the frequency-response functions. Specify a rectangular window with length equal to the burst period and no overlap between adjoining segments.
burstLen = 12000; [frf,f] = modalfrf(Xburst,Yburst,fs,burstLen);
Visualize a stabilization diagram and return the stable natural frequencies. Specify a maximum model order of 30 modes.
figure
modalsd(frf,f,fs,'MaxModes',30);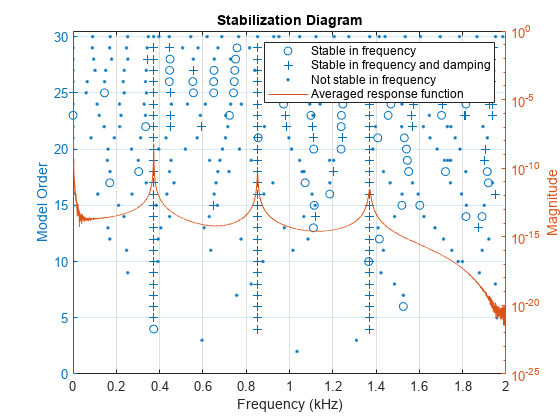
Zoom in on the plot. The averaged response function has maxima at 373 Hz, 852 Hz, and 1371 Hz, which correspond to the physical frequencies of the system. Save the maxima to a variable.
phfr = [373 852 1371];
Compute the modal parameters using the least-squares complex exponential (LSCE) algorithm. Specify a model order of 6 modes and specify physical frequencies for the 3 modes determined from the stabilization diagram. The function generates one set of natural frequencies and damping ratios for each input reference.
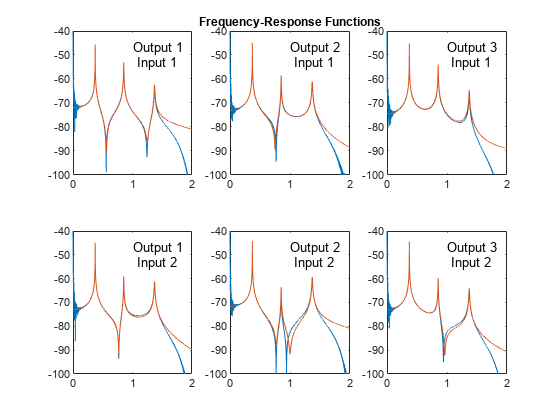
[fn,dr,ms,ofrf] = modalfit(frf,f,fs,6,'PhysFreq',phfr);Plot the reconstructed frequency-response functions and compare them to the original ones.
for k = 1:2 for m = 1:3 subplot(2,3,m+3*(k-1)) plot(f/1000,10*log10(abs(frf(:,m,k)))) hold on plot(f/1000,10*log10(abs(ofrf(:,m,k)))) hold off text(1,-50,[['Output ';' Input '] num2str([m k]')]) ylim([-100 -40]) end end subplot(2,3,2) title('Frequency-Response Functions')