SimBiology.RepeatDose
Define drug dosing protocol
Description
A SimBiology.RepeatDose object defines a series of doses to the amount of a
species during a simulation. The TargetName property of a dose object
defines the species that receives the dose.
Each dose is the same amount, as defined by the Amount property, and
given at equally spaced times, as defined by the Interval property. The
RepeatCount property defines the number of injections in the series,
excluding the initial injection. The Rate property defines how fast each
dose is given.
To use a dose object in a simulation you must add the dose object to a model object and
set the Active property of the dose object to true. Set the
Active property to true if you always want the dose to be applied before
simulating the model.
Warning
The Active property of the RepeatDose object will be removed in a future release. Explicitly specify a
dose or an array of doses as an input argument when you simulate a model using sbiosimulate.
When there are multiple active SimBiology.RepeatDose objects on a model and if
there are duplicate specifications for a property value, the last occurrence for the property
value in the array of dose, is used during simulation. You can find out which dose is applied
last by looking at the indices of the dose objects stored on the model.
You can set these dose properties to model parameters: Amount,
Interval, Rate, RepeatCount,
StartTime, LagParameterName and
DurationParameterName. You can set these properties, except
LagParameterName and DurationParameterName, to either
a numeric value or the name of a model-scoped parameter (as a character vector or string).
Parameterizing dose properties provides more flexibility for different dosing applications,
such as scaling the dose amount by body weight. For details, see Parameterized and Adaptive Doses.
Creation
You can create a SimBiology.RepeatDose object using any of the following functions.
adddose (model)— Creates a dose object and adds it to a model. You must set itsActiveproperty to true to apply the dose the model during simulation.sbiodose— Creates a standalone dose object that is not attached to any model. You can apply a standalone dose to different models during simulation by specifying the dose as a dosing input. UpdateTargetNameand other properties as appropriate when you are applying to different models.
For details, see Doses in SimBiology Models.
Properties
Active — Flag to use dose object during simulation
false or 0 (default) | true or 1
Flag to use the dose object during simulation, specified as a numeric or logical 1 (true) or 0 (false).
Data Types: double | logical
Amount — Dose amount
0 (default) | nonnegative scalar | character vector | string scalar
Dose amount, specified as a nonnegative scalar, character vector, or string scalar. The property defines an increase in the amount of a SimBiology® species that receives a dose.
You can parameterize the property by setting it to the name of a model-scoped parameter that is not being modified by a repeated assignment rule, an algebraic rule, or a rate rule. However, the parameter can be modified by an event.
A RepeatDose object defines a series of doses. Each dose is the
same amount, as defined by the Amount property, and given at equally
spaced times, as defined by the Interval property.
The number of injections in the series, excluding the initial injection, is defined
by the RepeatCount property, and the Rate property
defines how fast each dose is given.
Data Types: double | char | string
AmountUnits — Dose amount units
empty character vector (default) | character vector | string scalar
Dose amount units, specified as a character vector or string scalar.
This property defines units for the Amount property.
If the TargetName property defines a species, then AmountUnits for a dose must be a chemical amount (for example, milligram, mole, or molecule), not a concentration. To get a list of the defined units in the library, use the sbioshowunits function. To add a user-defined unit to the list, see sbioaddtolibrary.
Note
SimBiology uses units including empty units in association with DimensionalAnalysis and UnitConversion features.
When
DimensionalAnalysisandUnitConversionare bothfalse, units are not used. However, SimBiology still performs a minimum level of dimensional analysis to decide whether a reaction rate is in dimensions of amount/time or concentration/time.When
DimensionalAnalysisistrueandUnitConversionisfalse, units (if not empty) must have consistent dimensions so that SimBiology can perform dimensional analysis. However, the units are not converted.When
UnitConversionis set totrue(which requiresDimensionalAnalysisto betrue), SimBiology performs a dimensional analysis and converts everything to consistent units. Hence, you must specify consistent units, and no units can be empty. If you have a dimensionless parameter, you must still set its unit todimensionless.
Data Types: char | string
DurationParameterName — Parameter specifying length of time to administer a dose
empty character vector (default) | character vector | string scalar
Parameter specifying length of time to administer a dose, specified as a character vector or string scalar.
Specify the name of a parameter object that is scoped to a model. This parameter defines the length of time it takes to administer a dose.
You can parameterize the property by setting it to the name of a model-scoped parameter that is not being modified by a repeated assignment rule, an algebraic rule, or a rate rule. However, the parameter can be modified by an event.
Data Types: char | string
EventMode — Flag to determine whether to continue in-progress dosing
"stop" (default) | "continue"
Flag to determine whether to continue the in-progress dosing when an event changes a parameter that is referenced by a dose property, specified as "stop" or "continue".
If EventMode is set to "continue", the ongoing dose continues to completion when the event changes dose parameters, and updated parameters affect only subsequent doses. If EventMode is set to "stop", the ongoing dose stops immediately when dose parameters change, and subsequent doses use the updated parameters.
To decide whether a parameter has been changed, SimBiology compares the old value of a parameter to the new value. For instance, the following event does not change the doseStartTime parameter value: addevent(model,'time >= 5','doseStartTime = doseStartTime * 1').
Any change in dose parameters affects the schedule of doses generated. If an event changes dose parameters, SimBiology updates the dose schedule, ignores any doses scheduled before the current simulation time, and applies only the subsequent doses. Suppose that you have parameterized the StartTime property of a dose. Updating the parameter with an event causes to regenerate the dose schedule. If there are any previously-scheduled doses before the current simulation time, they are ignored.
By default, SimBiology uses the following MATLAB® expression to generate a list of dose times (dose schedule) whenever an event changes any dose parameter, using the updated parameter values:
,
where StartTime, RepeatCount, and Interval are properties of the dose object. Lag is the time lag parameter for a dose, referenced by the LagParameterName property.
Data Types: char | string
Interval — Time between doses
0 (default) | nonnegative scalar | character vector | string scalar
Time between doses, specified as a nonnegative scalar, character vector, or string scalar.
You can parameterize the property by setting it to the name of a model-scoped parameter that is not being modified by a repeated assignment rule, an algebraic rule, or a rate rule. However, the parameter can be modified by an event.
Note
When the Interval property is 0,
RepeatDose ignores the RepeatCount property,
that is, it treats it as though it is set to 0.
Data Types: double | char | string
LagParameterName — Parameter specifying time lag for dose
empty character vector (default) | character vector | string
Parameter specifying time lag for the dose, specified as a character vector or string scalar.
Specify the name of a parameter object that is scoped to a model. The parameter defines the length of time it takes for the dose to reach its target after being introduced.
You can parameterize the property by setting it to the name of a model-scoped parameter that is not being modified by a repeated assignment rule, an algebraic rule, or a rate rule. However, the parameter can be modified by an event.
Data Types: char | string
Name — SimBiology.RepeatDose object name
character vector | string
SimBiology.RepeatDose object name, specified as a character vector or string.
For details on requirements and recommendations for naming SimBiology components, see Guidelines for Naming Model Components.
Data Types: char | string
Notes — Additional information
empty character array (default) | character vector | string
Additional information that you can add for SimBiology.RepeatDose, specified as a
character vector or string.
Data Types: char | string
Parent — Parent object
SimBiology.Model object
This property is read-only.
Parent object, specified as a SimBiology.Model object.
The Parent property indicates accessibility of the object. The object is accessible to the Parent object and other objects within the Parent object.
Rate — Rate of dose
0 (default) | nonnegative scalar | character vector | string scalar
Rate of a dose, specified as a nonnegative scalar, character vector, or string scalar.
This property defines how fast a dose is given. If the rate is set to
0, then it is interpreted as a bolus (instantaneous) dose.
You can parameterize the property by setting it to the name of a model-scoped parameter that is not being modified by a repeated assignment rule, an algebraic rule, or a rate rule. However, the parameter can be modified by an event.
Note
If you set the Rate property of a dose, you must also specify
the Amount property of the dose, and set the
DurationParameterName property to ''. This is
because the duration is calculated from the amount and rate.
Tip
You can create a combination of bolus and infusion doses by setting the
rate property of a ScheduleDose object to a vector containing zeros and non-zeros.
Data Types: double | char | string
RateUnits — Units for dose rate
empty character vector (default) | character vector | string scalar
Units for the dose rate, specified as a character vector or string scalar.
You can use units from the units library with dimensions of amount divided by time, such as mole/second. You cannot use units of concentration divided by time, such as mole/liter/second.
Note
SimBiology uses units including empty units in association with DimensionalAnalysis and UnitConversion features.
When
DimensionalAnalysisandUnitConversionare bothfalse, units are not used. However, SimBiology still performs a minimum level of dimensional analysis to decide whether a reaction rate is in dimensions of amount/time or concentration/time.When
DimensionalAnalysisistrueandUnitConversionisfalse, units (if not empty) must have consistent dimensions so that SimBiology can perform dimensional analysis. However, the units are not converted.When
UnitConversionis set totrue(which requiresDimensionalAnalysisto betrue), SimBiology performs a dimensional analysis and converts everything to consistent units. Hence, you must specify consistent units, and no units can be empty. If you have a dimensionless parameter, you must still set its units todimensionless.
Data Types: char | string
RepeatCount — Dose repetitions
0 (default) | nonnegative integer | character vector | string scalar
Dose repetitions, specified as a nonnegative integer, character vector, or string scalar.
You can parameterize the property by setting it to the name of a model-scoped parameter that is not being modified by a repeated assignment rule, an algebraic rule, or a rate rule. However, the parameter can be modified by an event.
Data Types: double | char | string
StartTime — Start time for initial dose
0 (default) | nonnegative integer | character vector | string scalar
Start time for the initial dose, specified as a nonnegative integer, character
vector, or string scalar. For a series of repeated doses, the
StartTime property defines the amount of time that elapses before
the first (initial) dose is given.
You can parameterize the property by setting it to the name of a model-scoped parameter that is not being modified by a repeated assignment rule, an algebraic rule, or a rate rule. However, the parameter can be modified by an event.
Data Types: double | char | string
Tag — Object label
empty character array (default) | character vector | string
The object label, specified as a character vector or string.
Tip
Use this property to group objects and then use sbioselect to retrieve. For example, use the Tag property of reaction objects to group synthesis or degradation reactions. You can then retrieve all synthesis reactions using sbioselect. Similarly, for species objects you can enter and store classification information, for example, membrane protein, transcription factor, enzyme classifications, or whether a species is an independent variable. You can also enter the full form of the name of the species.
Data Types: char | string
TargetName — Name of species receiving dose
empty character vector (default) | character vector | string
Name of species receiving the dose, specified as a character vector or string scalar.
The dose amount increases the species amount at each time point or time interval defined by the dose.
The value of TargetName is the name of a species. If the model has more than one species with the same name, TargetName is defined as compartmentName.speciesName, where compartmentName is the name of the compartment containing the species.
Data Types: char | string
TimeUnits — Time units for dosing
empty character vector (default) | character vector | string scalar
Time units for dosing, specified as a character vector or string scalar. This
property specifies the units for the StartTime and
Interval properties.
If you change the value of the TimeUnits property, make sure that
you update the values of the StartTime and
Interval properties accordingly.
Data Types: char | string
Type — Object type
'repeatdose' (default)
This property is read-only.
Object type, specified as 'repeatdose'. When you create a
SimBiology object, the value of Type is automatically
defined.
Data Types: char
UserData — Data to associate with object
scalar | vector | string | ...
Data to associate with the object, specified as a numeric scalar, vector, string, or any other MATLAB data type.
The object does not use this data directly, but you can access it using dot notation or get.
Object Functions
copyobj | Copy SimBiology object and its children |
delete | Delete SimBiology object |
display | Display summary of SimBiology object |
get | Get SimBiology object properties |
getTable(ScheduleDose,RepeatDose) | Return data from SimBiology dose object as table |
rename | Rename SimBiology model component and update expressions |
set | Set SimBiology object properties |
setTable(ScheduleDose,RepeatDose) | Set dosing information from table to dose object |
Examples
Scale Dose Amount by Body Weight
Parameterize the Amount property of a dose to scale it by the body weight of a patient.
Create a simple model with linear elimination and an amount parameter.
model = sbiomodel('simple model'); compartment = addcompartment(model,'Central',1); compartment.CapacityUnits = 'liter'; species = addspecies(model,'drug'); species.InitialAmountUnits = 'milligram'; % Elimination rate elimParam = addparameter(model,'kel',0.1); elimParam.ValueUnits = '1/hour'; % Elimination reaction reaction = addreaction(model,'drug -> null'); reaction.ReactionRate = 'kel*drug'; amountParam = addparameter(model,'A',50); amountParam.ConstantValue = false; amountParam.ValueUnits = 'milligram'
amountParam = SimBiology Parameter Array Index: Name: Value: Units: 1 A 50 milligram
Create a dose with its Amount property set to the amount parameter 'A'.
dose = adddose(model,'adaptive dose','repeat'); dose.Amount = 'A';
Set other dose properties.
dose.TargetName = 'drug'; dose.StartTime = 0; dose.TimeUnits = 'hour'; dose.Interval = 24; dose.RepeatCount = 7;
Add a parameter to represent the body weight.
weightParam = addparameter(model,'weight', 80); weightParam.ValueUnits = 'kilogram';
Scale the dose amount by the body weight using an initial assignment rule.
scaleParam = addparameter(model,'doseAmountPerWeight',0.6); scaleParam.ValueUnits = 'milligram/kilogram'; rule = addrule(model,'A = weight*doseAmountPerWeight','initialAssignment');
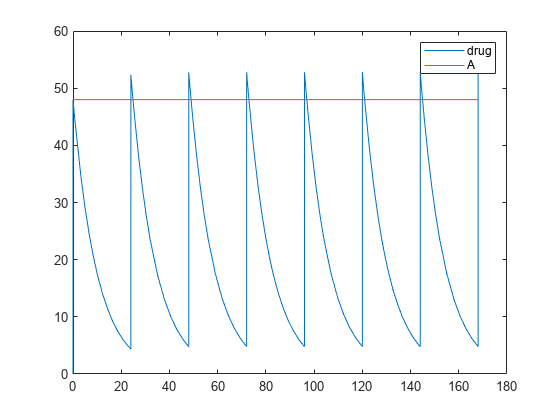
Simulate the model for 7 days and plot the results.
configset = getconfigset(model); configset.StopTime = 7*24; configset.TimeUnits = 'hour'; [time, drugAndAmount] = sbiosimulate(model,dose); plot(time, drugAndAmount); legend('drug','A');
Change Dose Behavior In Response to Changes in Model Parameters
Create a simple model with linear elimination, an amount parameter, and a rate parameter.
model = sbiomodel('simple model'); compartment = addcompartment(model,'Central',1); compartment.CapacityUnits = 'liter'; species = addspecies(model,'drug'); species.InitialAmountUnits = 'milligram'; % Elimination rate elimParam = addparameter(model,'kel',0.1); elimParam.ValueUnits = '1/hour'; % Elimination reaction reaction = addreaction(model,'drug -> null'); reaction.ReactionRate = 'kel*drug'; % Add amount and rate parameters amountParam = addparameter(model,'A',50); amountParam.ConstantValue = false; amountParam.ValueUnits = 'milligram'
amountParam = SimBiology Parameter Array Index: Name: Value: Units: 1 A 50 milligram
rateParam = addparameter(model,'R',10); rateParam.ValueUnits = 'milligram/hour'
rateParam = SimBiology Parameter Array Index: Name: Value: Units: 1 R 10 milligram/hour
Create a dose with its Amount and Rate properties set to the amount and rate parameters 'A' and 'R', respectively.
dose = adddose(model,'adaptive dose','repeat'); dose.Amount = 'A'; dose.Rate = 'R';
Set other dose properties.
dose.TargetName = 'drug'; dose.StartTime = 0; dose.TimeUnits = 'hour'; dose.Interval = 24; dose.RepeatCount = 7;
Prepare the configuration set to simulate the model for 7 days.
configset = getconfigset(model);
configset.StopTime = 7*24;
configset.TimeUnits = 'hour';Add an event to reset the dose amount to 10 at time >= 26.
event = addevent(model,'time >= 26','A = 10');
Set the EventMode property to 'stop'. This setting causes any ongoing dose event to stop at 26 hours.
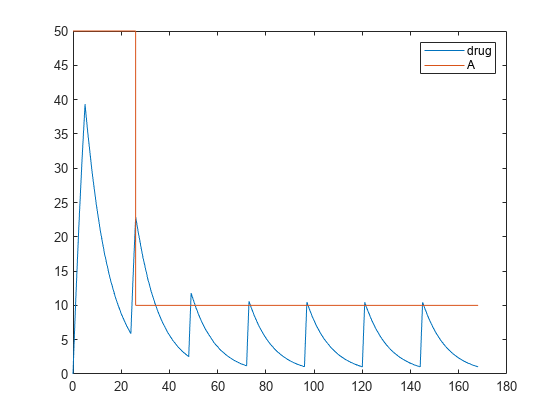
dose.EventMode = 'stop';Simulate the model. The second dose event stops at 26 hours, and the subsequent dose events continue with the new dose amount of 10.
[time, drugAndAmount] = sbiosimulate(model,dose); figure plot(time, drugAndAmount); legend('drug','A');
Alternatively, you can allow the ongoing dose event to finish before applying the new dose amount by setting EventMode to 'continue'.
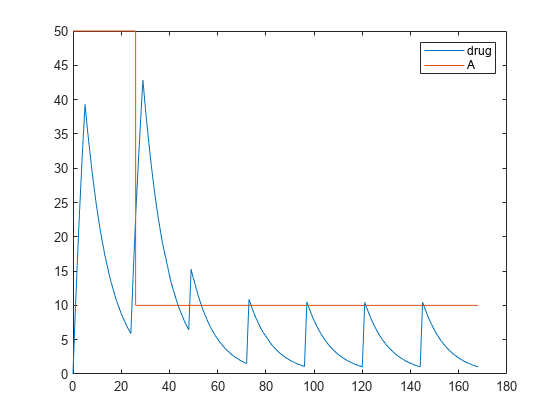
dose.EventMode = 'continue';Simulate the model. In this case, the second dose event continues to 26 hours.
[time, drugAndAmount] = sbiosimulate(model,dose); figure plot(time, drugAndAmount); legend('drug','A');
Change Dose Behavior In Response to Changes in Model Parameters
Create a simple model with linear elimination, an amount parameter, and a rate parameter.
model = sbiomodel('simple model'); compartment = addcompartment(model,'Central',1); compartment.CapacityUnits = 'liter'; species = addspecies(model,'drug'); species.InitialAmountUnits = 'milligram'; % Elimination rate elimParam = addparameter(model,'kel',0.1); elimParam.ValueUnits = '1/hour'; % Elimination reaction reaction = addreaction(model,'drug -> null'); reaction.ReactionRate = 'kel*drug'; % Add amount and rate parameters amountParam = addparameter(model,'A',50); amountParam.ConstantValue = false; amountParam.ValueUnits = 'milligram'
amountParam = SimBiology Parameter Array Index: Name: Value: Units: 1 A 50 milligram
rateParam = addparameter(model,'R',10); rateParam.ValueUnits = 'milligram/hour'
rateParam = SimBiology Parameter Array Index: Name: Value: Units: 1 R 10 milligram/hour
Create a dose with its Amount and Rate properties set to the amount and rate parameters 'A' and 'R', respectively.
dose = adddose(model,'adaptive dose','repeat'); dose.Amount = 'A'; dose.Rate = 'R';
Set other dose properties.
dose.TargetName = 'drug'; dose.StartTime = 0; dose.TimeUnits = 'hour'; dose.Interval = 24; dose.RepeatCount = 7;
Prepare the configuration set to simulate the model for 7 days.
configset = getconfigset(model);
configset.StopTime = 7*24;
configset.TimeUnits = 'hour';Add an event to reset the dose amount to 10 at time >= 26.
event = addevent(model,'time >= 26','A = 10');
Set the EventMode property to 'stop'. This setting causes any ongoing dose event to stop at 26 hours.
dose.EventMode = 'stop';Simulate the model. The second dose event stops at 26 hours, and the subsequent dose events continue with the new dose amount of 10.
[time, drugAndAmount] = sbiosimulate(model,dose); figure plot(time, drugAndAmount); legend('drug','A');

Alternatively, you can allow the ongoing dose event to finish before applying the new dose amount by setting EventMode to 'continue'.
dose.EventMode = 'continue';Simulate the model. In this case, the second dose event continues to 26 hours.
[time, drugAndAmount] = sbiosimulate(model,dose); figure plot(time, drugAndAmount); legend('drug','A');

Estimate Time Lag and Duration of a Dose
This example shows how to estimate the time lag before a bolus dose was administered and the duration of the dose using a one-compartment model.
Load a sample data set.
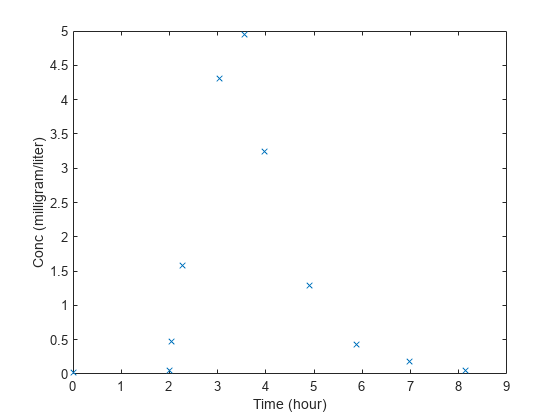
load lagDurationData.matPlot the data.
plot(data.Time,data.Conc,'x') xlabel('Time (hour)') ylabel('Conc (milligram/liter)')
Convert to groupedData.
gData = groupedData(data);
gData.Properties.VariableUnits = {'hour','milligram/liter'};Create a one-compartment model.
pkmd = PKModelDesign; pkc1 = addCompartment(pkmd,'Central'); pkc1.DosingType = 'Bolus'; pkc1.EliminationType = 'linear-clearance'; pkc1.HasResponseVariable = true; model = construct(pkmd); configset = getconfigset(model); configset.CompileOptions.UnitConversion = true;
Add two parameters that represent the time lag and duration of a dose. The lag parameter specifies the time lag before the dose is administered. The duration parameter specifies the length of time it takes to administer a dose.
lagP = addparameter(model,'lagP'); lagP.ValueUnits = 'hour'; durP = addparameter(model,'durP'); durP.ValueUnits = 'hour';
Create a dose object. Set the LagParameterName and DurationParameterName properties of the dose to the names of the lag and duration parameters, respectively. Set the dose amount to 10 milligram which was the amount used to generate the data.
dose = sbiodose('dose'); dose.TargetName = 'Drug_Central'; dose.StartTime = 0; dose.Amount = 10; dose.AmountUnits = 'milligram'; dose.TimeUnits = 'hour'; dose.LagParameterName = 'lagP'; dose.DurationParameterName = 'durP';
Map the model species to the corresponding data.
responseMap = {'Drug_Central = Conc'};Specify the lag and duration parameters as parameters to estimate. Log-transform the parameters. Initialize them to 2 and set the upper bound and lower bound.
paramsToEstimate = {'log(lagP)','log(durP)'};
estimatedParams = estimatedInfo(paramsToEstimate,'InitialValue',2,'Bounds',[1 5]);Perform parameter estimation.
fitResults = sbiofit(model,gData,responseMap,estimatedParams,dose,'fminsearch')fitResults =
OptimResults with properties:
ExitFlag: 1
Output: [1x1 struct]
GroupName: One group
Beta: [2x4 table]
ParameterEstimates: [2x4 table]
J: [11x2 double]
COVB: [2x2 double]
CovarianceMatrix: [2x2 double]
R: [11x1 double]
MSE: 0.0024
SSE: 0.0213
Weights: []
LogLikelihood: 18.7511
AIC: -33.5023
BIC: -32.7065
DFE: 9
DependentFiles: {1x2 cell}
Data: [11x2 groupedData]
EstimatedParameterNames: {'lagP' 'durP'}
ErrorModelInfo: [1x3 table]
EstimationFunction: 'fminsearch'
Display the result.
fitResults.ParameterEstimates
ans=2×4 table
Name Estimate StandardError Bounds
________ ________ _____________ ______
{'lagP'} 1.986 0.0051568 1 5
{'durP'} 1.527 0.012956 1 5
plot(fitResults)
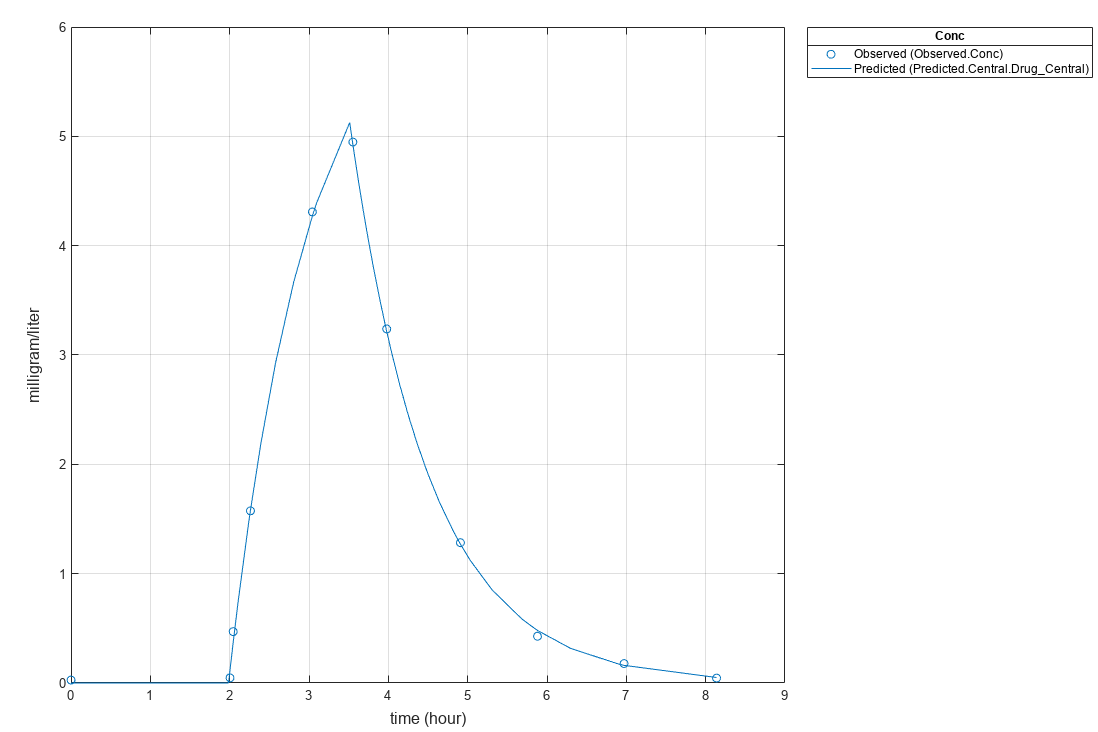
Version History
Introduced in R2010a
See Also
Model object | ScheduleDose object | sbiodose | sbiosimulate
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)