Model System Noise Figure
This example shows how to model system noise figure in RF Blockset™. RF receivers amplify signals and shift them to lower frequencies. The receiver itself introduces noise that degrades the received signal. The signal-to-noise ratio (SNR) at the receiver output ultimately determines the usability of the receiver.
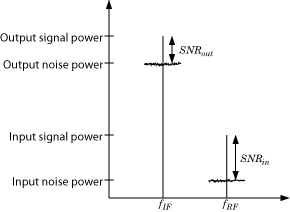
The preceding figure illustrates the effect of the receiver on the signal. The receiver amplifies a low-power RF signal at the carrier fRF with a high SNR and downconverts the signal to fIF. The noise figure (NF) of the system determines the difference between the SNR at the output and the SNR at the input:
SNR(out) = SNR(in) – NF(sys)
Where the difference is calculated in decibels. Excessive noise figure in the system causes the noise to overwhelm the signal, making the signal unrecoverable.
Create Low-IF Receiver Model
The model ex_simrf_snr_model simulates a simplified IF receiver architecture. A Sinusoid block and a Noise block model a two-tone input centered at fRF and low-level thermal noise. The RF system amplifies the signal and mixes it with the local oscillator fLO down to an intermediate frequency fIF. A voltage sensor recovers the signal at the IF.
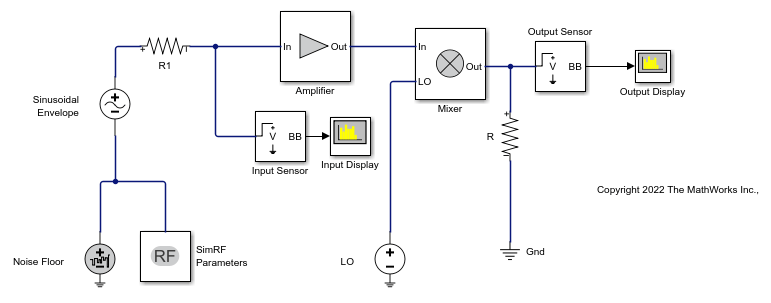
Setup RF Blockset Environment
To maximize performance, the Fundamental tones and Harmonic order parameters specify the simulation frequencies explicitly in the Configuration block:
fLO, the frequency of the LO in the first mixing stage, equals 1.9999 GHz. and appears in the list of fundamental tones as
carriers.LO.fRF, the carrier of the desired signal, equals 2 GHz and appears in the list of fundamental tones as
carriers.RF.fIF, the intermediate frequency, equals fRF – fLO. The frequency is a linear combination of the first-order (fundamental) harmonics of fLO and fRF. Setting Harmonic order to
1is sufficient to ensure this frequency appears in the simulation frequencies. This minimal value for the harmonic order ensures a minimum of simulation frequencies.
Solver conditions and noise settings are also specified for the Configuration block:
The Solver type is set to
auto. For more information on choosing solvers, see Configuration block.The Sample time parameter is set to
1/(mod_freq*64). This setting ensures a simulation bandwidth 64 times greater than the envelope signals in the system.The Simulate noise box is checked, so the environment includes noise parameters during simulation.
The model uses subsystems with a MATLAB Coder™ implementation of a fast Fourier transform (FFT) to generate two plots. The FFT uses 64 bins, so for a sampling frequency of 64 Hz, the bandwidth of each bin is 1 Hz. Subsequently, the power levels shown in the figures also represent the power spectral density (PSD) of the signals in dBm/Hz.
View Simulation Output
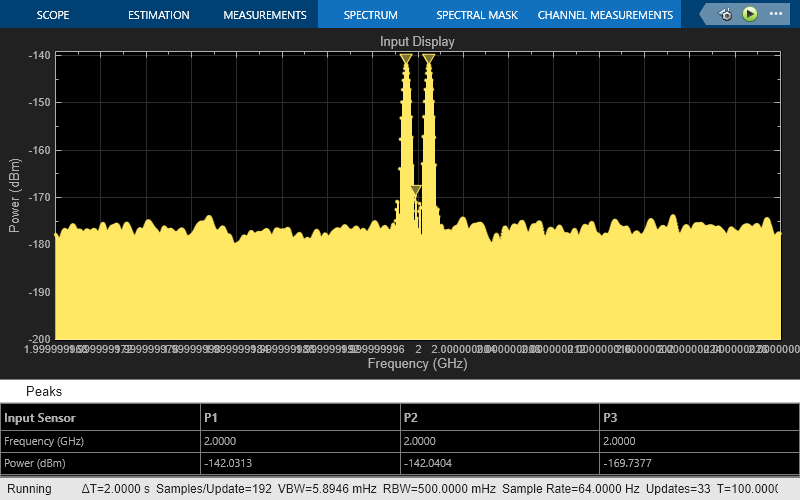
The Input Display plot shows the power spectrum of the signal and noise at the input of the receiver. The measured power of each tone is consistent with the expected power level of a 0.1vμV two-tone envelope:
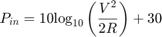
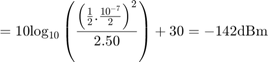
A factor of 1/2 is due to voltage division across source and load resistors, and another factor of 1/2 is due to envelope scaling. For more information on scaling envelope signals for power calculation, see Two-Tone Envelope Analysis Using Real Signals. The measured noise floor at -177 dBm/Hz is reduced by 3 dB from the specified -174 dBm/Hz noise floor. The difference is due to power transfer from the source to the input of the amplifier. The amplifier also models a thermal noise floor, so although this decrease is unrealistic, it does not affect accuracy at the output stage.
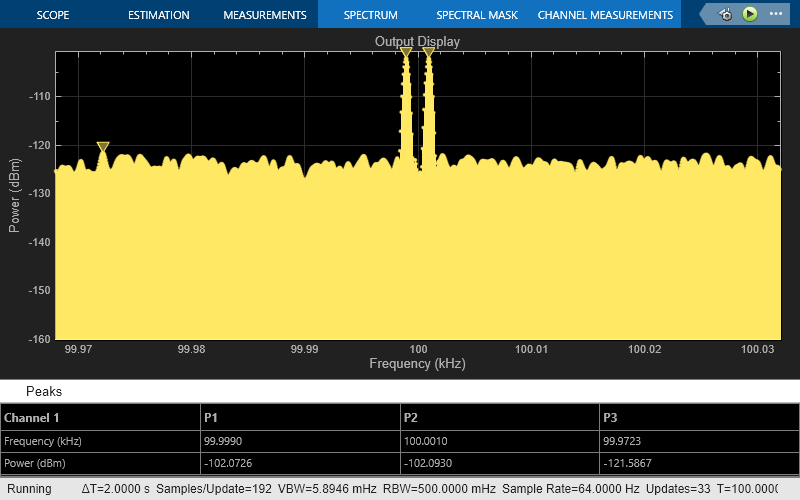
The Output Display plot shows the power spectrum of the signal and noise at the output of the receiver. The measured PSD of –102 dBm/Hz for each tone is consistent with the 40-dB combined gain of the amplifier and mixer. The noise PSD in the figure is shown to be approximately 50 dB higher at the output, due to the gain and noise figure of the system.
Simulate Thermal Noise Floor
Thermal noise power can be modeled according to the equation,
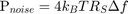
where:
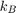 is Boltzmann's constant, equal to
is Boltzmann's constant, equal to 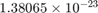 J/K.
J/K.
T is the noise temperature, specified as 293.15 K in this example.
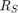 is the noise source impedance, specified as 50 ohm in this example to agree with the resistance value of the Resistor block labeled R1.
is the noise source impedance, specified as 50 ohm in this example to agree with the resistance value of the Resistor block labeled R1.
Δf is the noise bandwidth.
To model the noise floor on the RF signal at the resistor, the model includes a Noise block:
The *Noise Power Spectral Density (Watts/Hz) parameter is calculated as 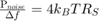 . The *Carrier frequencies parameter, set to
. The *Carrier frequencies parameter, set to carriers.RF , places noise on the RF carrier only.
Compute System Noise Figure
To model RF noise from component noise figures:
Select Simulate noise in the RF Blockset Parameters block dialog box, if it is not already selected.
Specify a value for the Noise figure (dB) parameter of an Amplifier and Mixer blocks.
The noise figures are not strictly additive. The amplifier contributes more noise to the system than the mixer because it appears first in the cascade. To calculate the total noise figure of the RF system with n stages, use the Friis equation:
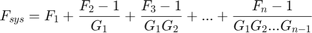
where Fi and Gi are the noise factor and gain of the ith stage, and NFi = 10log10(Fi).
In this example, the noise figure of the amplifier is 10 dB, and the noise figure of the mixer is 15 dB, so the noise figure of the system is:

The Friis equation shows that although the mixer has a higher noise figure, the amplifier contributes more noise to the system.
