Sine Wave
Generate sine wave, using simulation time as time source
Libraries:
Simulink /
Sources
Description
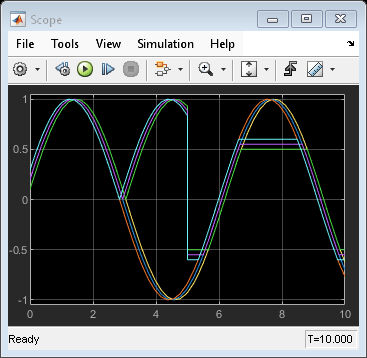
The Sine Wave block outputs a sinusoidal waveform. The block can operate in time-based or sample-based mode.
Note
This block is the same as the Sine Wave Function block that
appears in the Math Operations library. If you select Use external
signal for the Time parameter in the block
dialog box, you get the Sine Wave Function block.
Time-Based Mode
The block calculates the output waveform.
In time-based mode, the value of the Sample time parameter determines whether the block operates in continuous mode or discrete mode.
0(the default) causes the block to operate in continuous mode.>0causes the block to operate in discrete mode.
For more information, see Specify Sample Time.
When operating in continuous mode, the Sine Wave block can become inaccurate due to loss of precision as time becomes very large.
A Sample time parameter value greater than zero causes the block to behave as if it were driving a Zero-Order Hold block whose sample time is set to that value.
This way, you can build models with sine wave sources that are purely discrete, rather than models that are hybrid continuous/discrete systems. Hybrid systems are inherently more complex and as a result take more time to simulate.
In discrete mode, this block uses a differential incremental algorithm instead of one based on absolute time. As a result, the block can be useful in models intended to run for an indefinite length of time, such as in vibration or fatigue testing.
The differential incremental algorithm computes the sine based on the value computed at the previous sample time. This method uses the following trigonometric identities:
In matrix form, these identities are:
Because Δt is constant, the following expression is a constant:
Therefore, the problem becomes one of a matrix multiplication of the value of by a constant matrix to obtain .
Discrete mode reduces but does not eliminate the accumulation of round-off errors. This accumulation can happen because computation of the block output at each time step depends on the value of the output at the previous time step.
To handle round-off errors when the Sine Wave block operates in time-based discrete mode, use one of these methods.
| Method | Rationale |
|---|---|
|
Insert a Saturation block directly downstream of the Sine Wave block. |
By setting saturation limits on the Sine Wave block output, you can remove overshoot due to accumulation of round-off errors. |
|
Set up the Sine Wave block to use the
|
The |
Sample-Based Mode
Sample-based mode uses this formula to compute the output of the Sine Wave block.
A is the amplitude of the sine wave.
p is the number of time samples per sine wave period.
k is a repeating integer value that ranges from 0 to p–1.
o is the offset (phase shift) of the signal.
b is the signal bias.
In this mode, Simulink® sets k equal to 0 at the first
time step and computes the block output, using the formula. At the next time step,
Simulink increments k and recomputes the output of the
block. When k reaches p, Simulink resets k to 0 before computing
the block output. This process continues until the end of the simulation.
The sample-based method of computing block output at a given time step does not depend on
the output of the previous time steps. Therefore, this mode avoids the accumulation
of round-off errors. Sample-based mode supports reset semantics in subsystems that
offer it. For example, if a Sine Wave block is in a resettable
subsystem that receives a reset trigger, the repeating integer k
resets and the block output resets to its initial condition.
Examples
Ports
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Extended Capabilities
Version History
Introduced before R2006a