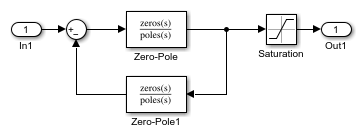
Zero-Pole
Model system using zero-pole-gain transfer function
Libraries:
Simulink /
Continuous
Description
The Zero-Pole block models a system that you define by specifying the zeros, poles, and gain of a Laplace-domain transfer function. You can use this block to model single-input single-output (SISO) and single-input multiple-output (SIMO) systems.
The Zero-Pole block has these requirements:
The transfer function must have the form
where Z represents the zeros, P represents the poles, and K represents the gain of the transfer function.
The number of poles must be greater than or equal to the number of zeros.
Complex poles and zeros must be complex-conjugate pairs.
For a multiple-output system, all transfer functions must have the same poles. The zeros can differ in value, but the number of zeros for each transfer function must be the same.
Tip
To model a multiple-output system in which the transfer functions have different numbers of zeros or a single zero each, use multiple Zero-Pole blocks.
Model Single-Output Systems
A single-output system has scalar time-domain input and output signals. To model this type of system:
Enter a vector for the zeros of the transfer function in the Zeros field.
Enter a vector for the poles of the transfer function in the Poles field.
Enter a scalar for the gain of the transfer function in the Gain field.
Model Multiple-Output Systems
A multiple-output system has a scalar time-domain input signal and a vector time-domain output signal. Each element in the vector output is an output of the system. To model this type of system:
Enter a matrix of zeros in the Zeros field.
Each column of the matrix contains the zeros of a transfer function that relates the system input signal to one of the elements in the output signal.
Enter a vector for the poles common to all transfer functions of the system in the Poles field.
Enter a vector of gains in the Gain field.
Each element is the gain of the corresponding transfer function in the zeros matrix.
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Tips
The appearance of the transfer function in the Zero-Pole block icon depends on how you specify the zero, pole, and gain parameters.
If you specify each parameter as an expression or a vector, the block shows the transfer function with the specified zeros, poles, and gain. If you specify a variable in parentheses, the block evaluates the variable.
For example, the image shows how the block looks when you specify the Zeros parameter as
[3 2 1], the Poles parameter as(poles), wherepolesis a variable with the value[7 5 3 1], and the Gain parameter asgain.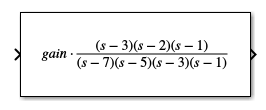
If you specify each parameter as a variable, the block shows the name of the variable that defines the value for the Gain parameter followed by a generic transfer function.
For example, the image shows how the block looks when you specify the Zeros parameter as the variable
zeros, the Poles parameter as the variablepoles, and the Gain parameter as the variablegain.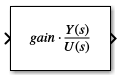
When the block is not large enough to display the transfer function using the parameter values, the transfer function is shown with a numerator of
zeros(s)and a denominator ofpoles(s).
Extended Capabilities
Version History
Introduced before R2006a