Characteristics of Lookup Table Data
Sizes of Breakpoint Vectors and Table Data
The following constraints apply to the sizes of breakpoint vectors and table data associated with lookup table blocks:
The memory limitations of your system constrain the overall size of a lookup table.
Lookup tables must use consistent dimensions so that the overall size of the table data reflects the size of each breakpoint vector.
To illustrate the second constraint, consider the following vectors of input and output values that create the relationship in the plot.
Vector of input values: [-3 -2 -1 0 1 2 3] Vector of output values: [-3 -1 0 -1 0 1 3]
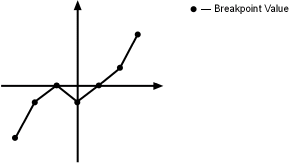
In this example, the input and output data are the same size (1-by-7), making the data consistently dimensioned for a 1-D lookup table.
The following input and output values define the 2-D lookup table that is graphically shown.
Row index input values: [1 2 3] Column index input values: [1 2 3 4] Table data: [11 12 13 14; 21 22 23 24; 31 32 33 34]
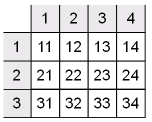
In this example, the sizes of the vectors representing the row and column indices are 1-by-3 and 1-by-4, respectively. Consequently, the output table must be of size 3-by-4 for consistent dimensions.
Monotonicity of Breakpoints
The first stage of a table lookup operation involves relating inputs to the breakpoints. The search algorithm requires that input breakpoint sets be strictly monotonically increasing, that is, each successive element is greater than its preceding element. For example, the vector
A = [0 0.5 1 1.9 2.1 3]
is a valid breakpoint vector as each element is larger than its predecessors.
Note
Although a breakpoint vector is strictly monotonic in
double format, it might not be so after conversion to a
fixed-point data type.
Formulation of Evenly Spaced Breakpoints
You can represent evenly spaced breakpoints in a data set by using one of these methods.
| Formulation | Example | When to Use This Formulation |
|---|---|---|
[first_value:spacing:last_value] | [10:10:200] | The lookup table does not use
double or single. |
first_value + spacing *
[0:(last_value-first_value)/spacing] | 1 + (0.02 * [0:450]) | The lookup table uses double or
single. |
Because floating-point data types cannot precisely represent some numbers, the
second formulation works better for double and
single. For example, use 1 + (0.02 *
[0:450]) instead of [1:0.02:10]. For a list of
lookup table blocks that support evenly spaced breakpoints, see Summary of Lookup Table Block Features.
Among other advantages, evenly spaced breakpoints can make the generated code division-free and reduce memory usage. For more information, see:
fixpt_evenspace_cleanupin the Simulink® documentationEffects of Spacing on Speed, Error, and Memory Usage (Fixed-Point Designer)
Identify questionable fixed-point operations (Embedded Coder)
Tip
Do not use the MATLAB®
linspace function to define evenly spaced breakpoints.
Simulink uses a tighter tolerance to check whether a breakpoint set has
even spacing. If you use linspace to define breakpoints for
your lookup table, Simulink considers the breakpoints to be unevenly spaced.
